《高等数学》课程教学资源（课件讲稿）第八章 向量代数与空间解析几何_0802数量积 向量积

第八章向量代数与空间解析几何第二节数量积只向量积两向量的数量积两向量的向量积08

第八章 向量代数与空间解析几何 第二节 数量积 向量积 一、两向量的数量积 二、两向量的向量积

引言1、二阶行列式a12a1定义日由四个数排成一行二列（横排称行、竖排称列)的数表a21a22称为二阶行列式数a,称为行列式的第i行第i列的元素，i为行标，i为列标aa12计算： D == aiα22 - a12^21a21a222、三阶行列式定义由九个数排成三行三列（横排称行、竖排称列）的数表anla13a122α23称为三阶行列式,a21a31a32a33o个不个高等数学教学部不不个

高等数学教学部 2

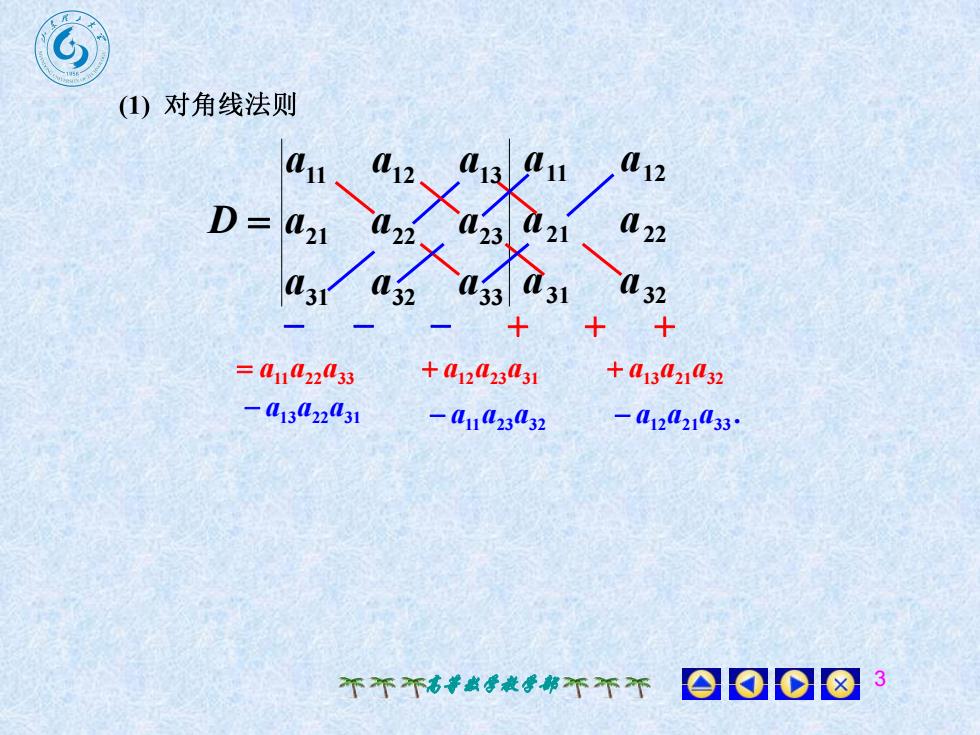
(1)对角线法则a12ana12an113D=a22(21a22a23a21a31a321'32d31a'33+++=a1122433+a13a21a32+a12a2331-a13/2231-anA23ll32-ai2a21a33:3008个个个高等数学教学部不不不

高等数学教学部 3 31 32 21 22 11 12 a a a a a a   31 32 33 21 22 23 11 12 13 a a a a a a a a a D   a11a23a32  a11a22a33      a12a23a31  a13a21a32 .  a12a21a33  a13a22a31

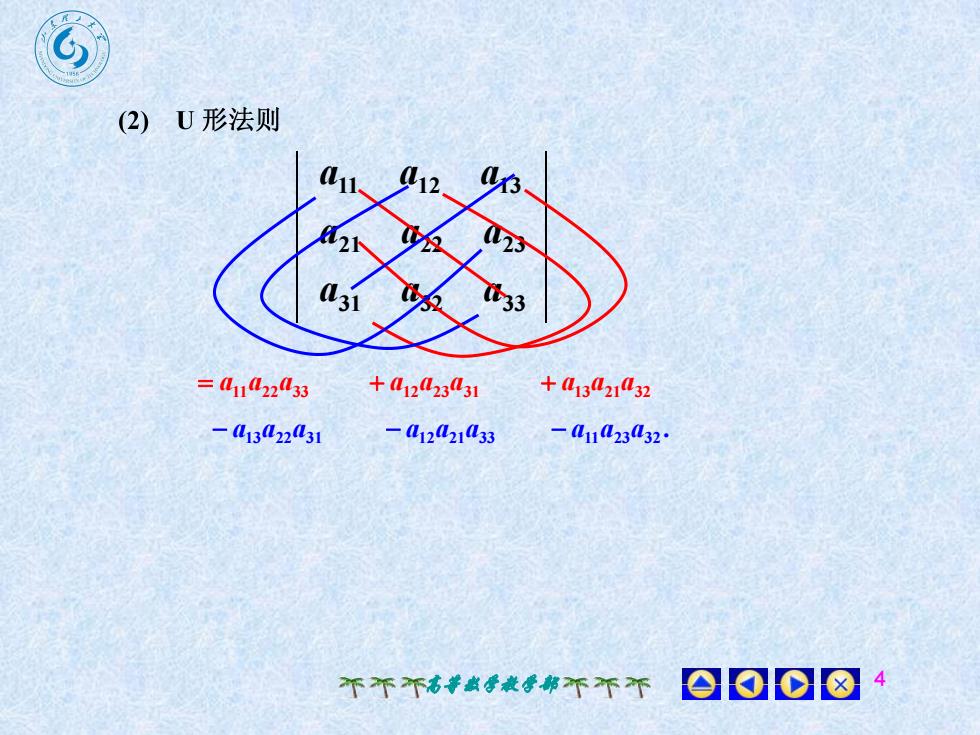
(2)U 形法则aX3aua12(2321(31033= ai1a22l33+a12a23a31+13a2132 a13(22A31- a1221l33- a11a23A32:0010个个个高等数学教学部个不个

高等数学教学部 4 31 32 33 21 22 23 11 12 13 a a a a a a a a a  a11a22a33 .  a11a23a32  a12a23a31  a13a21a32  a13a22a31  a12a21a33

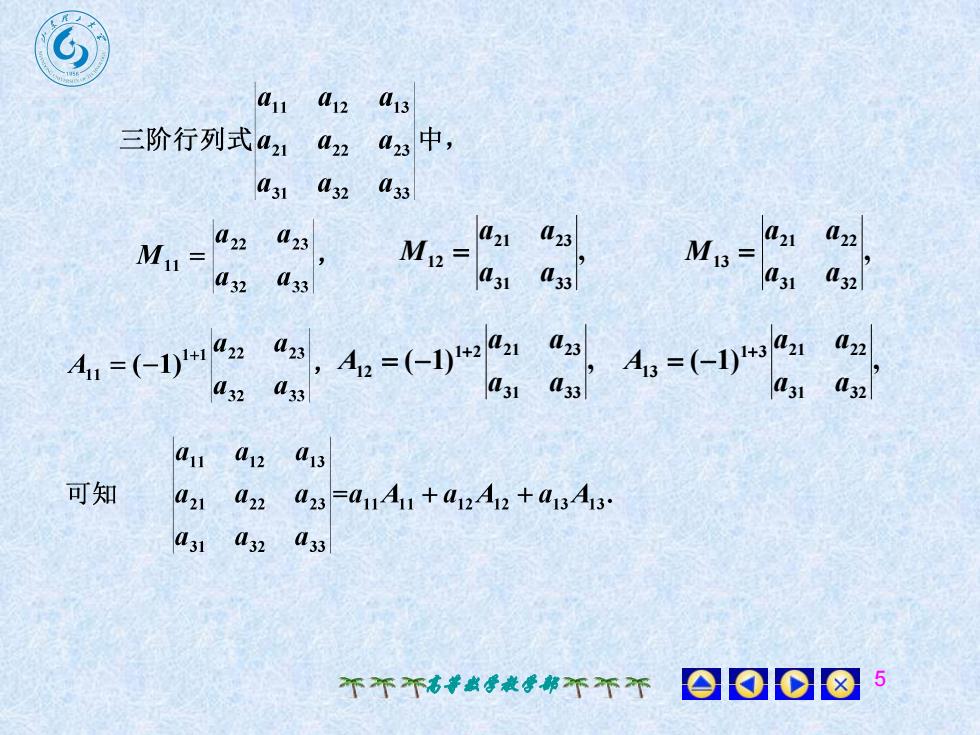
Caia12a13中,三阶行列式a21a23a22a31a33a32a21a21a22a123a22a23M13Mi2 =Mi-a31a33a32a31a33a32a21a21a22a23a22a23A13 =(-1)1+3A12 =(-1)1+2A =(-1)+1a31a31(33a32a32a33aua12a13可知a21a22=a11A11 +a12A12 +a13A13a23a31a32a33oo8个个个高等数学教学部不不不

高等数学教学部 5 , 31 33 21 23 12 a a a a M  , 31 32 21 22 13 a a a a M  ( 1) , 31 33 1 2 21 23 12 a a a a A    ( 1) , 31 32 1 3 21 22 13 a a a a A   