
第八章向量代数与空间解析几何第四节空间直线及其方程空间直线的一般方程空间直线的对称式方程及参数方程三直线的两点式方程四五直线与直线的夹角福直线与平面的夹角六、平面束08
第八章 向量代数与空间解析几何 第四节 空间直线及其方程 一、空间直线的一般方程 二、空间直线的对称式方程及参数方程 三、直线的两点式方程 四、直线与直线的夹角 五、直线与平面的夹角 六、平面束
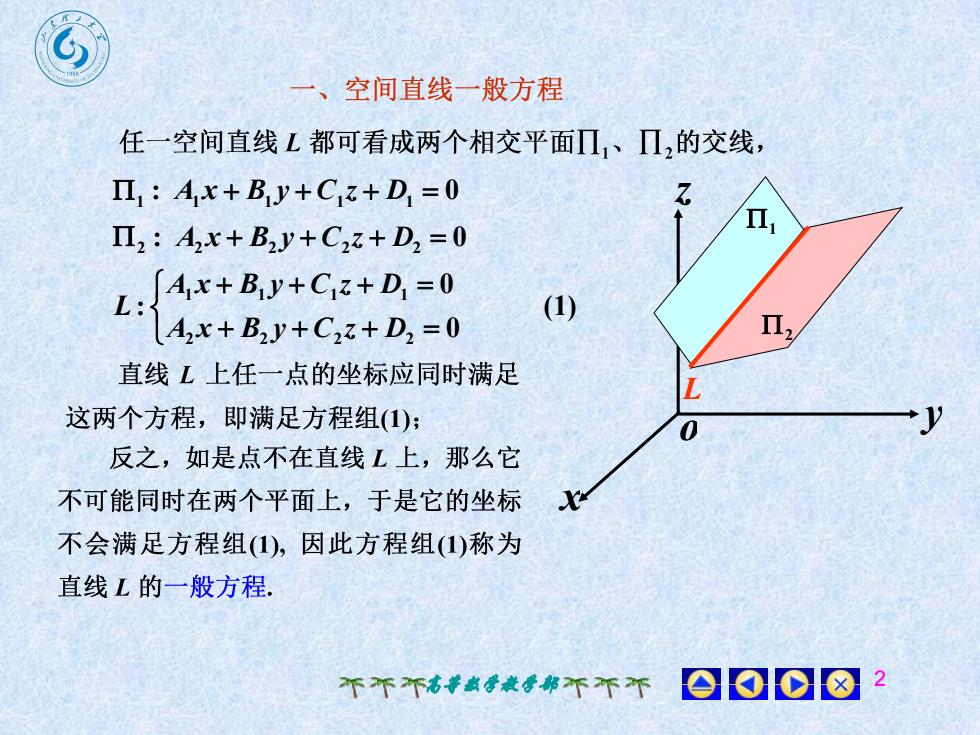
?、空间直线一般方程任一空间直线L都可看成两个相交平面II、II,的交线I,: Ax+By+Cz+D =0ZIIII, : A,x+B,+C,z+ D, = 0[Ax+By+Cz+D, = 0(1)L :II,A,x+ B,y+C,z+ D, = 0直线L上任一点的坐标应同时满足LJ这两个方程,即满足方程组(1);0反之,如是点不在直线L上,那么它X不可能同时在两个平面上,于是它的坐标不会满足方程组(1),因此方程组(1)称为直线L的一般方程008中个不个高等数学教学部不不个
高等数学教学部 2 x y z o 1 2 1 : A1 x B1 y C1z D1 0 2 : A2 x B2 y C2z D2 0 (1) 0 0 : 2 2 2 2 1 1 1 1 A x B y C z D A x B y C z D L L
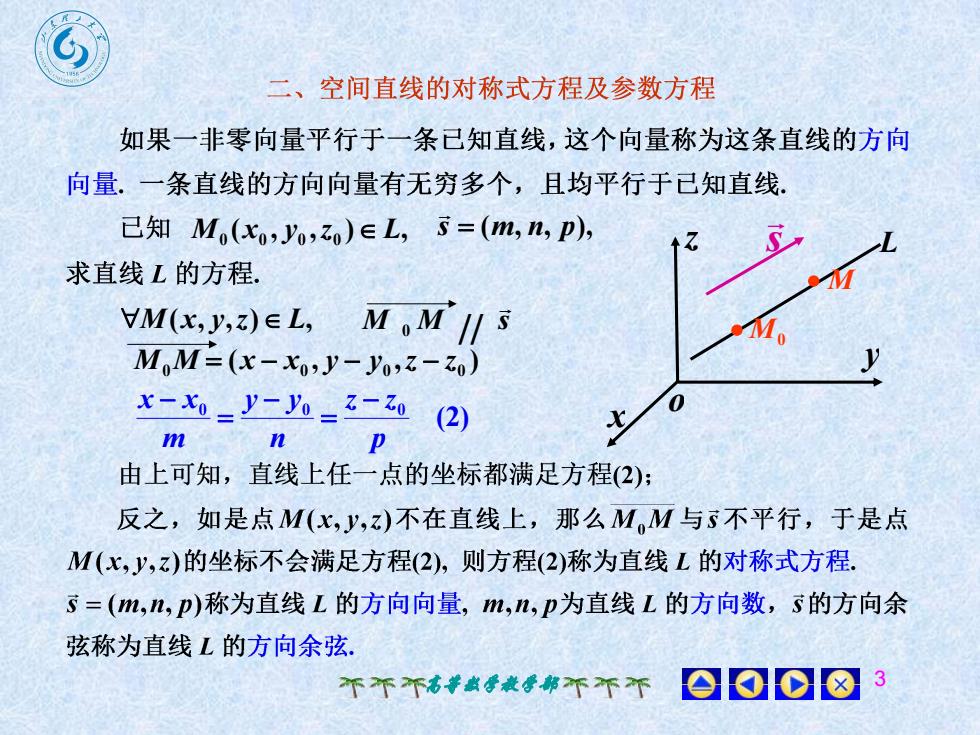
-空间直线的对称式方程及参数方程如果一非零向量平行于一条已知直线,这个向量称为这条直线的方向向量.一条直线的方向向量有无穷多个,且均平行于已知直线已知 M,(xo,yo,z)e L, s =(m, n, p),S1zL求直线L的方程MVM(x, y,z)e L,M.MI/sRM.yM,M=(x-xo,y- yo,z-zo)0x -xo -y- yo - z- zo(2)XmnP由上可知,直线上任一点的坐标都满足方程(2);反之,如是点M(x,y,z)不在直线上,那么M.M与s不平行,于是点M(x,y,z)的坐标不会满足方程(2),则方程(2)称为直线L的对称式方程s=(m,n,p)称为直线 L的方向向量,m,n,p为直线L的方向数,s的方向余弦称为直线L的方向余弦0008个个个高数学教学部不不不
高等数学教学部 3 x y z o s L M0 M ( , , ) , M0 x0 y0 z0 L M(x, y,z) L, M M s 0 // s (m, n, p), ( , , ) 0 0 0 0 M M x x y y z z (2) 0 0 0 p z z n y y m x x

+x-xoy-yoZ-z0今=tnmpx= X, +mt可得直线的参数方程y= yo +nt .z = zo + pt说明在式(2)中,若有个别分母为零,应理解为相应的分子也为零x-x,=0x-xoy-yoZ-Z0如可理解为寸3y-yo_z-zo,0nppnx-x,=0x-xoz-zoy-yo可理解为00(y-y, =0po8个不个高数学教学部不不个
高等数学教学部 4 , 0 0 0 t p z z n y y m x x . 0 0 0 z z pt y y nt x x mt , 0 0 0 0 p z z n x x y y , 0 0 0 0 p z z n y y x x , 0 0 0 0 0 p x x y y z z . 0 0 0 0 y y x x

?x+y+z+1=0例1用对称式方程及参数方程表示直线[2x - y + 3z + 4 = 0解在直线上任取一点(x,yo,z),取x,=1,代入方程得[y,+z, +2 = 0lJ。- 3z -6 = 0解得 y=0,zo=-2,点坐标(1,0,-2)取s = n, ×n, =(4,-1,-3),x =1+ 4tx-1 y-0 z+2y=-t#-3’4-1[z = -2 - 3too8个个个高等数学教学部不不不
高等数学教学部 5 . 2 3 4 0 1 0 x y z x y z ( , , ), 0 0 0 x y z , 3 6 0 2 0 0 0 0 0 y z y z (4,1,3), , 3 2 1 0 4 1 x y z . 2 3 1 4 z t y t x t