
第九章多元函数微分法及其应用第八节多元函数的极值及其求法多元函数的极值及其最大值、最小值条件极值拉格朗日乘数法08
第九章 多元函数微分法及其应用 第八节 多元函数的极值及其求法

福引言设函数 f(x)在点x.的某邻域U(x.)内有定义.如果对于去心邻域U(x)内的任一点x,有f(x)< f(x)(或f(x)>f(x,)),则称f(x,)是函数fx)的一个极大值(或极小值)设函数f(x)在点x,处可导,且在x,处取得极值,那么f'(x)=0设函数f)在点x.处连续,且在x的某去心邻域Ux,S)内可导(1) 若xE(x, -S,x,)有 f(x)>0;而xe(x,,x,+)有 f'(x)<0, 则f(x)在x,处取得极大值(2) 若xe(x,-S,x,)有f'(x)<0;而xe(x,x,+8)有 f'(x)>0,则f(x)在x,处取得极小值(3) 如果当xe(x-S,x)及x(x,x,+S)时,f'(x)符号相同,则f(x)在x,处无极值001018个不不高教学教学部不不不
高等数学教学部 2

(第二充分条件)设f(x)在x.处具有二阶导数,且 f'(x)=0f"(x,)±0,那么(1)当f"(x,)<0时,函数f(x)在x,处取得极大值;(2)当f"(x,)>0时,函数f(x)在x,处取得极小值福0008个个个高等数学教学部
高等数学教学部 3

、多元函数的极值及其最大值、最小值1、极值的定义定义 设函数z= f(x,)的定义域为D,P(x,y)为 D 的内点.如果存在P.的某个邻域U(P)CD,使得对于该邻域内异于P的任何点(x,y),都有 f(x,y)< f(x,y.),则称函数z= f(x,y)在点(x,yo)有极大值,点(xoy)称为函数z=f(x,J)的极大值点;如果对于该邻域内异于P的任何点(x,y),都有f(x,y)>f(xo,y),则称函数z=f(x,j)在点(x,Jo)有极小值,点(x,y)称为函数z= f(x,y)的极小值点极大值、极小值统称为极值,使函数取得极值的点称为极值点推广 设 n 元函数u=f(P)的定义域为 D,P,是 D 的内点。若存在P的某个邻域U(P)C D,使得该邻域内异于P的任何点 P,都有f(P)<f(P) (或f(P)> f(P))则称函数f(P)在点P有极大值(或极小值)f(P)001018个不不高尊数学教学部不不
高等数学教学部 4
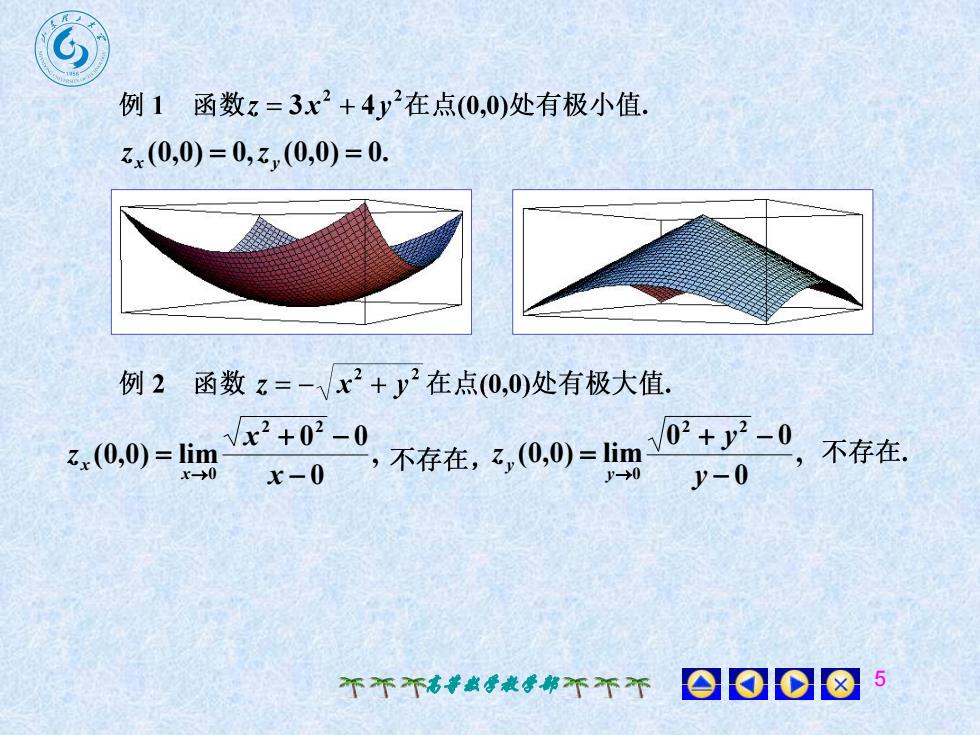
例1 函数z=3x2+4在点(0,0)处有极小值zx(0,0) = 0,z,(0,0) = 0例 2函数 z=-x2+2在点(0,0)处有极大值/x2+02- 002 + y?不存在。,不存在,z,(0,0)=limz. (0,0) = limx-0y-0x-→0y-050008个个个高数学教学部不不个
高等数学教学部 5 (0,0) 0, (0,0) 0. x y z z , 0 0 0 (0,0) lim 2 2 0 x x z x x , 0 0 0 (0,0) lim 2 2 0 y y z y y