《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0904多元复合函数的求导法则

第九章多元函数微分法及其应用第四节多元复合函数的求导法则0

第九章 多元函数微分法及其应用 第四节 多元复合函数的求导法则

一元函数与多元函数复合的情形如果u=g(x)在点x 可导，而y= f(u)在点u=g(x)可导，则复合函数y=fIg(x))在点x可导，且dydydy du或f'(u)·g'(x)dxdxdu dx定理1若函数u=@(t),v=(t)在点t可导，函数z=f(u,v)在对应点(u,μ)具有连续偏导数，则复合函数z=flβ(t), (t)I在点 t 可导，且有dzOz duOz dvdt Ou dt Ov dt0008中个不不高教学教学部不不不

高等数学教学部 2 f (u) g (x) dx dy     . dx du du dy dx dy 或  

定理1 若函数u=(t),v=(t)在点 t 可导，函数z=f(u,)在对应点(u,)具有连续偏导数，则复合函数z= flβ(t), (t))在点 t 可导，且有dz du Oz dydt ou dt Ow dt证设t取增量△t，则u、相应有增量△u,△v,z相应有增量△z.因z= f(u,v)在点(u,)处具有连续偏导数，则z= f(u,v)可微Ozaz由微分定义知，△zAu+△v+o(p) , (p = (u)2 +(△v)2)avQuAzOz AuOz Avo(p).. limlimav AtAtAt-0 △tt→0 Ou NtOz AuOzAvo(p)= limOu NtOv △tAt-→0pOz du.oz dv1Ov dtOu dt001018个不高等教学教学部不不不

高等数学教学部 3 z u v t t z t    0 lim   ) ( ) lim( 0 t o t v v z t u u z t                ] | | ( ) ( ) ( ) lim[ 2 2 0 t t t v t o u t v v z t u u z t                         . dt dv v z dt du u z        

推论若函数u=(t),v=y(t),w=の(t)在点 t 可导，函数z=f(u,v,w)在对应点(u,v,w)具有连续偏导数，则复合函数z=flp(t),y (t),の(t)在点t可导，且有dz Oz duOz dv Oz dwdt Ou dt Oy dt aw dt0008个不个高尊数学教学部不不不

高等数学教学部 4 z u v w t

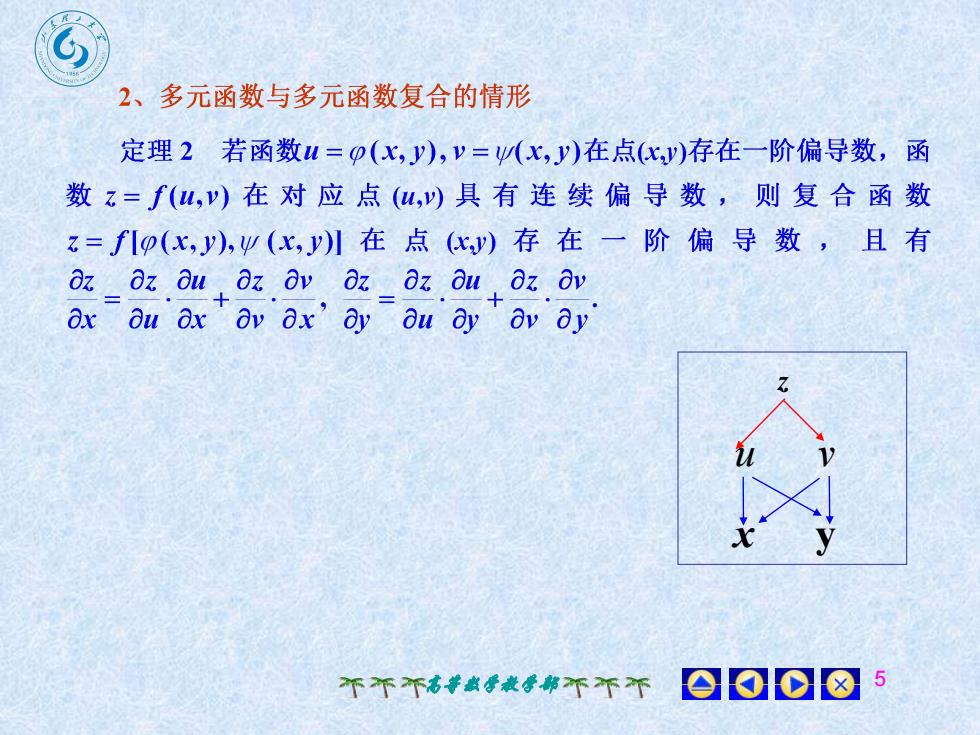
2、多元函数与多元函数复合的情形定理2 若函数u=β(x,),V=y(x,y)在点(x,)存在一阶偏导数，函数z=f(u,v)在对应点(u,")具有连续偏导数，则复合函数z=flp(x,y),y(x,y)) 在点 (x) 存在 一阶 偏 导数，且有Ozz OuOz Ovzz OuOz Ovax au ax v ax' ay Qu ay av ay000?不不不高尊数学教学部不不不

高等数学教学部 5 z u v x y