
第三章第七节平面曲线的曲率主要内容:一、弧微分曲率及其计算公式三、 E曲率圆与曲率半径
第七节 主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径 平面曲线的曲率 第三章

一、弧微分设 = f(x)在(α,b)内有连续导数,ty= f(x)在曲线y=f(x)上取固定点M。(xo,yo)MoM作为度量弧长的基点,并规定依x增大s=s(x)的方向作为曲线的正向.对曲线上任Xoxx一点M(x,y),规定有向弧段M.M的值s(简称为弧s):s的绝对值等于这弧段的长度,当有向弧段MM的方向与曲线的正向一致时s>0.相反时s<0:s=s(x)是x的单调增加的函数.下面求s(x)的导数及微分
一、 弧微分 设 在(a , b)内有连续导数, 并规定依 增大 的方向作为曲线的正向. x O y f ( x) x y 0 x M0 x 0 0 0 M 在曲线 ( ) ( , ) 上取固定点 作为度量弧长的基点, y f x M x y 0 ( , ), ( ) : 对曲线上任 一点 规定有向弧段 的值 简称为弧 M x y M M s s s s x ( ) s的 绝 对 值 等 于 这 弧 段 的 长 度 , 0 0, 0. 当有向弧段 的方向与曲线的正向一致时 相反时 M M s s s s x x ( ) . 是 的 单 调 增 加 的 函 数 下 面 求 s x ( ) . 的 导 数 及 微 分

一、弧微分设 = f(x)在(α,b)内有连续导数,其图形为 AByy= f(x)弧长 S= AM = s(x)BMMM'AsMM'AxMM'△xMM" /(Ax)? +(Ay)axLbxMM'△xx+△xMM'MM'?+lim=±1MM'AX-0MM'= /1+()2: s(x)= limAx-0Ax
一、 弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s A M s( x) x s M M M M x M M M M M M x x y 2 2 ( ) ( ) M M M M 2 1 ( ) x y x s s x x 0 ( ) lim 2 1 ( y ) x O y f ( x) A B a b x y x M x x M y lim 1 0 M M M M x

s(x)= /1+(y)2: ds= /1+(y)?dx 或 ds = /(dx)? +(dy)x =p(t)福若曲线由参数方程表示y=y(t)则弧长微分公式为 ds=Vo"(t)+y"2(t)d tds =|MT几何意义:Idy= /(dx) + (dy)?VdxQxx+dxx
则弧长微分公式为 2 2 d ( ) ( ) d s φ t ψ t t ds 1 ( y ) dx 2 或 2 2 ds ( dx) ( dy) O x dx dx x y x M dy T 几何意义: ds MT 2 2 ( ) ( ) . d d x y 若曲线由参数方程表示: ( ) ( ) x t y t
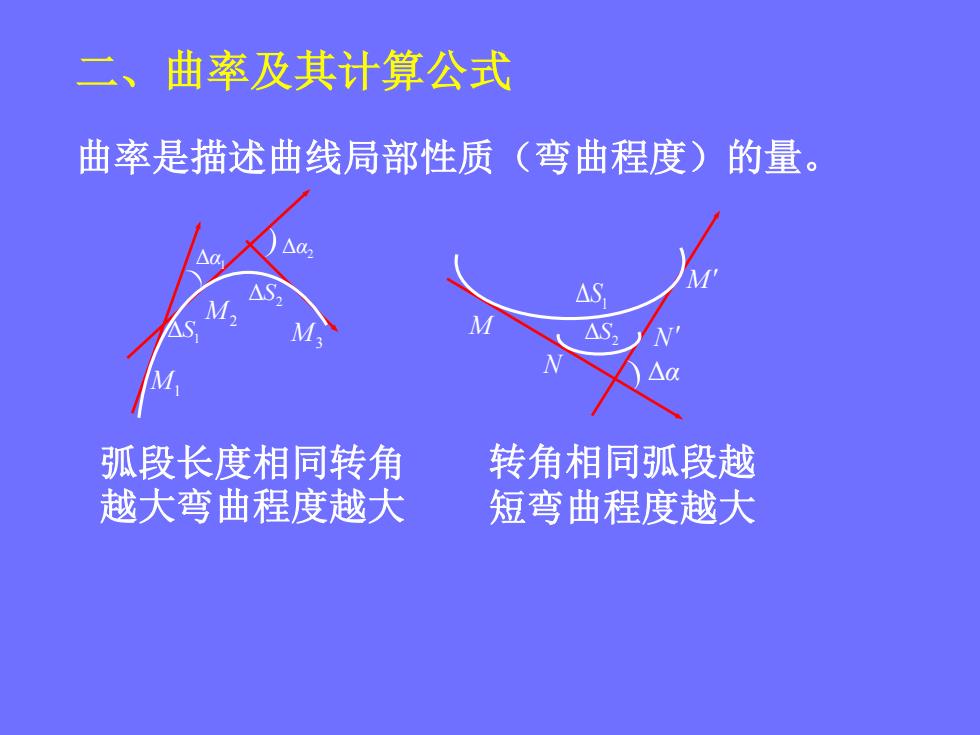
二、曲率及其计算公式曲率是描述曲线局部性质(弯曲程度)的量。Na2AaMAS,AS2M2SLASMAAa转角相同弧段越弧段长度相同转角越大弯曲程度越大短弯曲程度越大
二、曲率及其计算公式 曲率是描述曲线局部性质(弯曲程度)的量。 M1 M3 Δα2 M2 Δ 2 S Δ 1 S M M Δ 1 S Δ 2 S N N Δα 弧段长度相同转角 越大弯曲程度越大 转角相同弧段越 短弯曲程度越大 Δα1