
第三节第四章分部积分法由导数公式(uv)'= u'v+uv积分得:uv = [u'vdx + [ u'dx[u'dx=uv- [u'vdx分部积分公式或「udv=uv-Jvdu选取u及(或dv)的原则:1)v容易求得;2)[u'vdx比[uv'dx容易计算
第三节 由导数公式 (uv) u v uv 积分得: uv u vdx uv dx 分部积分公式 uv dx uv u v dx 或 ud v uv v d u 1) v 容易求得 ; 容易计算 . 分部积分法 第四章
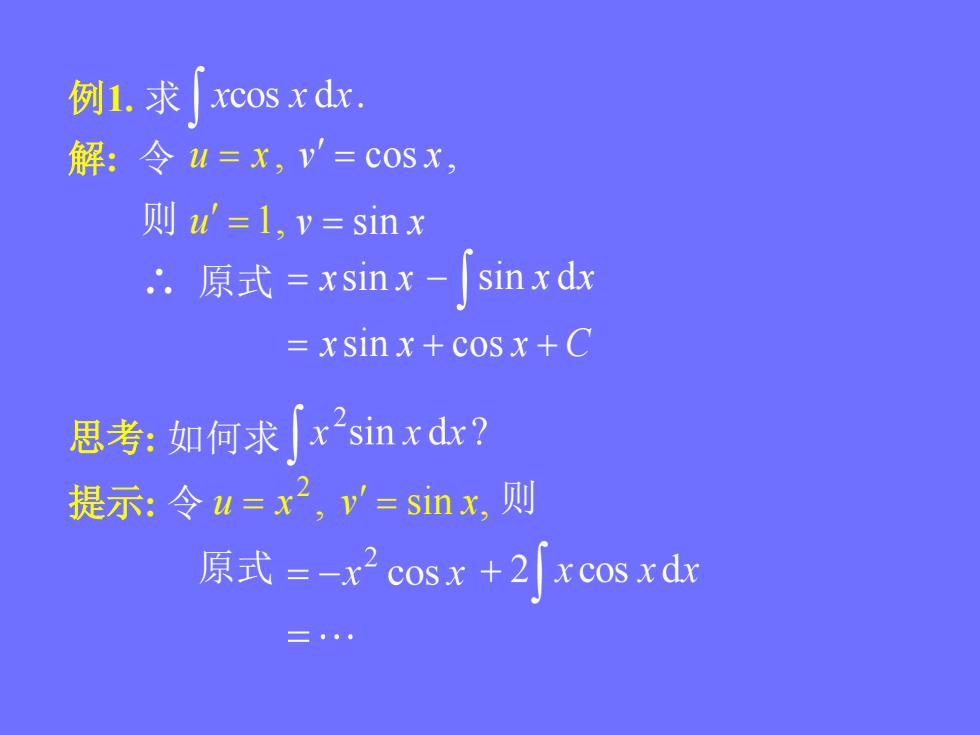
xcos x dx.例1.求解:令u=x,v=cosx,则u'=l,v=sinxsinx dx: 原式 =xsinx-=xsinx+cosx+Cxsinxdx?思考:如何求提示:令u=x2,'= sin x,则原式 =-x2 cosx +2[xcos xdx
例1. 求 解: 令 u x , v cos x , 则 u 1, v sin x ∴ 原式 x sin x sin x dx x sin x cos x C 思考: 如何求 提示: 令 , 2 u x v sin x, 则 原式
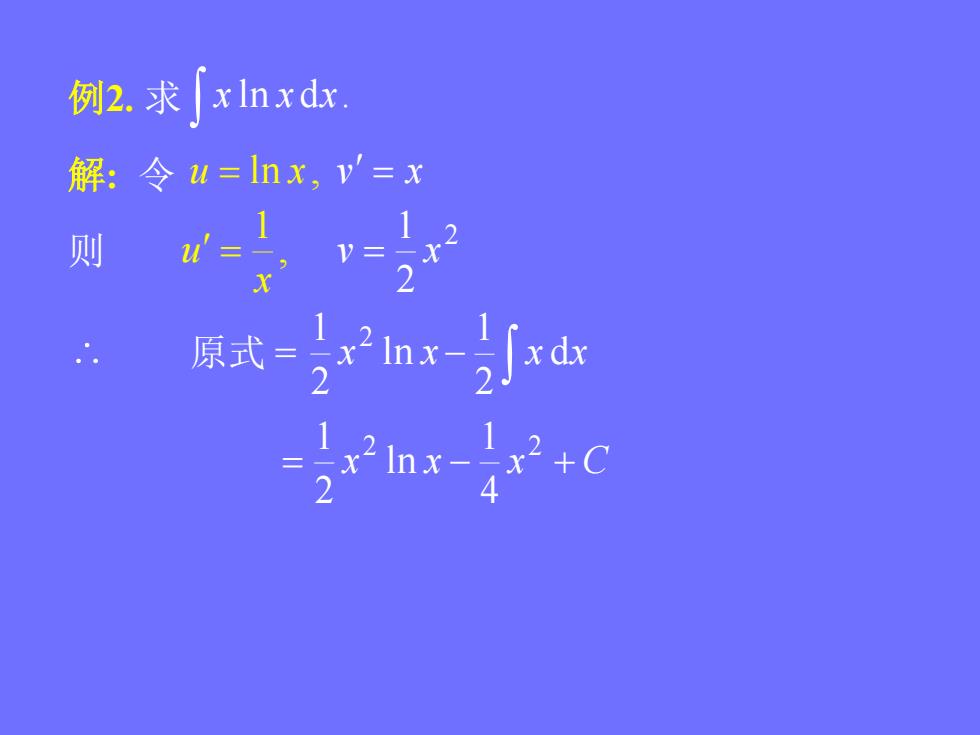
例2.求[xln xdx.解:令u=lnx,=x则原式:xdx
例2. 求 x ln x dx. 解: 令 u ln x , v x 则 , 1 x u 2 2 1 v x 原式 = x ln x 2 1 2 x dx 2 1 x x x C 2 2 4 1 ln 2 1

x arctan x dx例3.求解:令u=arctanx,v'= x则·原式arctanx1福dxarctan x21-x-arctan x)+CarctanxC
例3. 求 x arctan x dx. 解: 令 u arctan x , v x 则 , 1 1 2 x u 2 2 1 v x ∴ 原式 x arctan x 2 1 2 x x x d 2 1 1 2 2 x arctan x 2 1 2 x x ) d 1 1 (1 2 1 2 x arctan x 2 1 2 (x arctan x) C 2 1

例4.求「esinxdx解:令u=sinx,v'=ex,则u'= cosx, v=er原式=e*sinx-[ecosxdx再令u=cosx,v=e*则u'=-sinx, v=ex=e"sin x -e"cos x-[e"sinx dx故原式= e*(sinx-cosx)+C说明:也可设u=ev为三角函数,但两次所设类型必须一致
例4. 求 e sin x dx. x 解: 令 u sin x , x v e , 则 u cos x , x v e ∴ 原式 x x e sin x x x e cos d 再令 u cos x , x v e , 则 u sin x , x v e x x e sin x x x x x e cos e sin d 故 原式 = x x C x e (sin cos ) 2 1 说明: 也可设 为三角函数 , 但两次所设类型 必须一致