
第三节泰勒公式一、泰勒公式的建立二、几个初等函数的麦克劳林公式三、泰勒公式的应用
二、几个初等函数的麦克劳林公式 第三节 一、泰勒公式的建立 三、泰勒公式的应用 泰勒公式
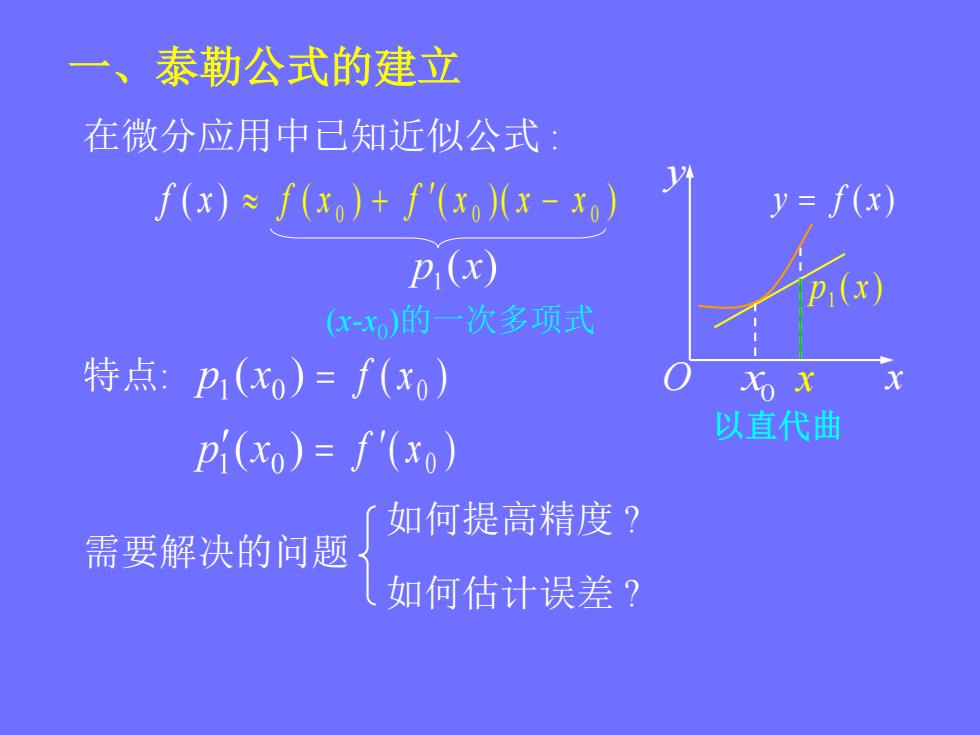
一、泰勒公式的建立在微分应用中已知近似公式:y= f(x)f(x) = f(xo)+ f'(x。)(x-xo)pi(x)p,(x)(x-xo)的一次多项式特点: Pi(xo)= f(xo)XoxX以直代曲pi(xo) = f(xo)如何提高精度?需要解决的问题如何估计误差?
特点: ( ) 0 f x ( ) 0 f x 一、泰勒公式的建立 f ( x ) ( ) ( ) ( ) 0 0 0 f x f x x x 以直代曲 x0 ( ) 1 p x 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x (x-x0 )的一次多项式 x y y f ( x) O
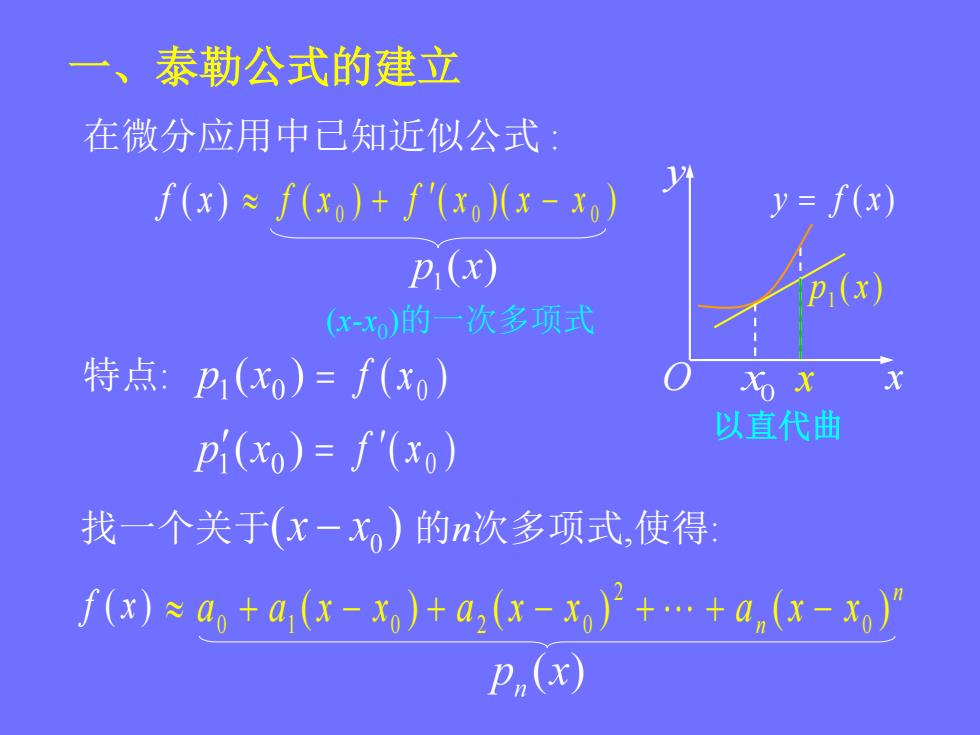
一、泰勒公式的建立在微分应用中已知近似公式:y= f(x)f(x)= f(xo)+ f'(xo)(x-xop;(x)pi(x)(x-xo)的一次多项式特点: Pi(xo)= f(xo)XX x以直代曲pi(xo) = f'(xo)找一个关于(x一x)的n次多项式,使得f(x) =ao +a,(x-x)+a,(x-x)?+.. +a,(x-xo)p,(x)
特点: ( ) 0 f x ( ) 0 f x 一、泰勒公式的建立 f ( x ) ( ) ( ) ( ) 0 0 0 f x f x x x 以直代曲 x0 ( ) 1 p x 在微分应用中已知近似公式 : x (x-x0 )的一次多项式 x y y f ( x) O 找一个关于 的n次多项式,使得: f ( x ) 2 0 1 0 2 0 0 ( ) ( ) ( ) n n a a x x a x x a x x

1.求n次近似多项式Pn(x),要求:pn(xo)=f(xo),pn(xo)= f(xo), ..,pm(xo)=f(n)(xo)pn(x) = ao+ ai(x - xo)+ a2(x - xo) +... +an(x - xo)ai+ 2a2(x - xo)+.. + nan(x- xo)n-1则pn(x)=2la2 +..+n(n-1)an(x-xo)n-2pn(x) =n!anp(m)(x) =aj=pn(xo)= f'(xo),ao=Pn(xo)=f(xo)a2 =P"(xo)=f"(xo), * ,an =pm)(xo)= f(n)(xo)故Pakya f( f$yo(as tre t)(xod(txxo)3+ ..+(xo)
f ( x ) 2 0 1 0 2 0 0 ( ) ( ) ( ) n n a a x x a x x a x x 1. 求 n 次近似多项式 要求: ( ) 2! 0 1 2 a p x n ( ), 0 f x , ( ) 0 ( ) ! 1 a p x n n n n ( ) 0 ( ) f x n 故 pn ( x) ( ) 0 f x ( ) ( ) 0 0 f x x x 2! 1 ! 1 n n n f ( x ) ( x x ) 0 0 ( ) ! 1 n 2 0 0 f ( x ) ( x x ) 2! 1 pn ( x) 则 pn ( x) pn ( x) n ( ) n!a ( ) p x n n ( ) 0 0 a p x n ( ), 0 f x ( ) 1 0 a p x n ( ), 0 f x a1 2 ( ) 2 0 a x x 1 0 ( ) n n n a x x 2 2 !a 2 0 ( 1) ( ) n n n n a x x a0 n n a ( x x ) a ( x x ) a ( x x ) 0 2 1 0 2 0

泰勒(Taylor)中值定理:若f(x)在包含xo的某开区间(a,b)内具有直到n+1阶的导数,则当xE(a,b)时,有F() = f(x0) + f(x0)(x - xo) + I"(x0)+-2!(x0)(x- xo)"+ R,(x)n!f(n+) (E)其中R(x)=(x -xo)n+1(在Xo与x之间)(n+1)!公式①称为fx)的n阶泰勒公式公式②称为n阶泰勒公式的拉格朗日余项泰勒
公式 ① 称为 的 n 阶泰勒公式 . 公式 ② 称为n 阶泰勒公式的拉格朗日余项 . 泰勒(Taylor)中值定理 : 阶的导数 , 时, 有 ( ) 0 f x ( ) ( ) 0 0 f x x x 2 0 0 ( ) 2 ! ( ) x x f x n n x x n f x ( ) ! ( ) 0 0 ( ) R ( x) n ① 其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) n n n x x n f R x ② 则当 ) 0 ( 在 x 与 x 之 间 泰勒