
复变函数关于定义的说明:(1)如果C是闭曲线,那么沿此闭曲线的积分记为f(z)dz.(2)如果C是x轴上的区间a≤x≤b,而 f(z)=u(x),这个积分定义就是一元实变函数定积分的定义
6 关于定义的说明: ( )d . (1) , C f z z C 记为 如果 是闭曲线 那么沿此闭曲线的积分 . ( ), (2) , ( ) 定积分的定义 这个积分定义就是一元实变函数 如果 是 轴上的区间 而 u x C x a x b f z =

复变函数二、积分存在的条件及其计算法1.存在的条件如果 f(z)是连续函数而C是光滑曲线时积分cf(z)dz一定存在.证?设光滑曲线C由参数方程给出z=z(t)=x(t)+iy(t), α≤t≤β正方向为参数增加的方向参数α及βB对应于起点A及终点B.u
7 二、积分存在的条件及其计算法 1. 存在的条件 ( )d . ( ) , 积分 一定存在 如果 是连续函数而 是光滑曲线时 C f z z f z C 证 z = z(t) = x(t) + i y(t), t 设光滑曲线C由参数方程给出 正方向为参数增加的方向, 参数 及 对应于起点 A及终点 B

复变函数并且 z'(t)≠ 0, α<t< β,如果 f(z)=u(x,y)+iv(x,J)在D内处处连续那么u(x,J)和v(x,J)在D内均为连续函数,设Sk=5k+ink因为△z= Zk= Zk-1 = X +iyk-(Xk-1 +iyk-1)=(Xk - Xk-1)+i(yk - yk-1)=Axk +iAyk,U
8 并且 z (t) 0, t , 如果 f (z) = u(x, y) + i v(x, y)在 D内处处连续, 那么u(x, y)和v(x, y)在 D内均为连续函数, , k k k 设 = + i ( ) k = k − k−1 = k + k − k−1 + k−1 因为 z z z x iy x iy ( ) ( ) = k − k−1 + k − k−1 x x i y y , k k = x + iy

复变函数nZf(5k) Azk所以k=1Z[u(5k, nk) + iv(5k,nk)1(Axk + iAyk)=k=1nE[u(k,nk)Axk -v(5k,nk)Ayh]k=1E[v(5k,nk)Axk + u(5k,nk)AYk]+k=1由于u,V都是连续函数根据线积分的存在定理u
9 k n k k f z =1 所以 ( ) = = + + n k k k k k k k u i v x i y 1 [ ( , ) ( , )]( ) = = + + = − n k k k k k k k n k k k k k k k i v x u y u x v y 1 1 [ ( , ) ( , ) ] [ ( , ) ( , ) ] 由于u, v 都是连续函数, 根据线积分的存在定理
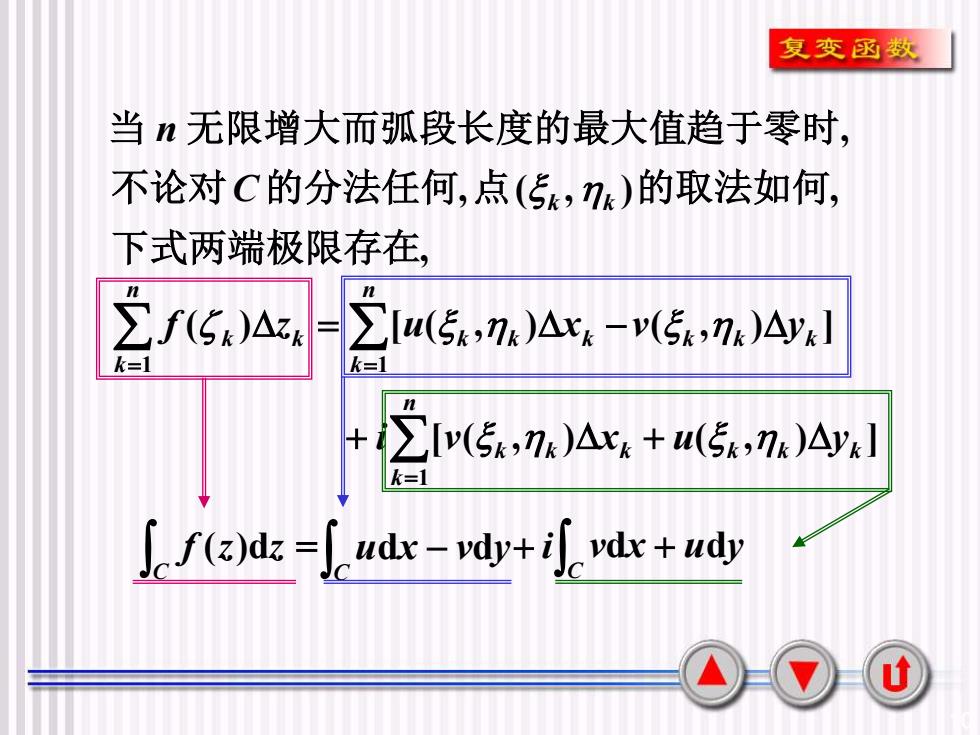
复变函数当n无限增大而弧段长度的最大值趋于零时不论对C的分法任何,点(Sk,nk)的取法如何,下式两端极限存在Ef(Sk)AzkE[u(Ek,nk)Axk -v(5k,nk)Ayk]=k=1k=1E[v(Ek,nk)Axk + u(5k,nk)Ayk]k=fc f(z)dz =J udx - ydy+if. ydx + udyU
10 当 n 无限增大而弧段长度的最大值趋于零时, , , ( , ) , 下式两端极限存在 不论对C的分法任何 点 k k 的取法如何 = = = + + = − n k k k k k k k n k k k k k k k n k k k i v x u y f z u x v y 1 1 1 [ ( , ) ( , ) ] ( ) [ ( , ) ( , ) ] C f (z)dz − C udx vdy + C = + i vdx udy