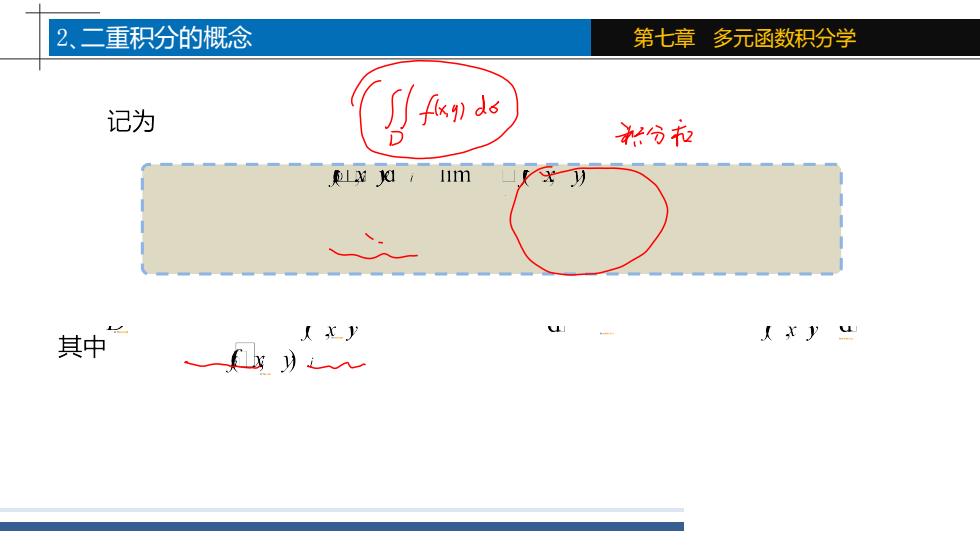
2、二重积分的概念 第七章多元函数积分学 记为 状分拉 L灯1m 其中“ 人北y 人xy4
2、二重积分的概念 第七章 多元函数积分学

可积的充分条件及几何意义 第七章多元函数积分学 如果二重积分 人xy D fxy D D D 定理1在区域 上的修a的一宁 第可a的 很容易知道,当J“ 聪八.14V 0x)0 )d f x y 代教红
可积的充分条件及几何意义 第七章 多元函数积分学

第七章多元函数积分学 ,0Σz 例1用二重积分表示上半球体 5的生性的 上半球面可以看成是以 1湿7-51 z=1-x2-y2 故 图7-5 和,2对yx 其中
第七章 多元函数积分学 D x 2+y 2≤1 1 1 y x O z z= 1 x 2 y 2 - -

第七章多元函数积分学 东嗣:用:重和分春衣=+疗与=4所国立惭
第七章 多元函数积分学

3、二重积分的性质 第七章多元函数积分学 二重积分和定积分有着相似的性质,以下性质均假设被积函数在所在区域上 可积性 飞f+19k)16-b06+wd6 性质1 线4性 性质2 ∫-d6 =一川f96 D=D,UP2 性质3设DD,D2 [E域可性 6d 0 x
3、二重积分的性质 第七章 多元函数积分学