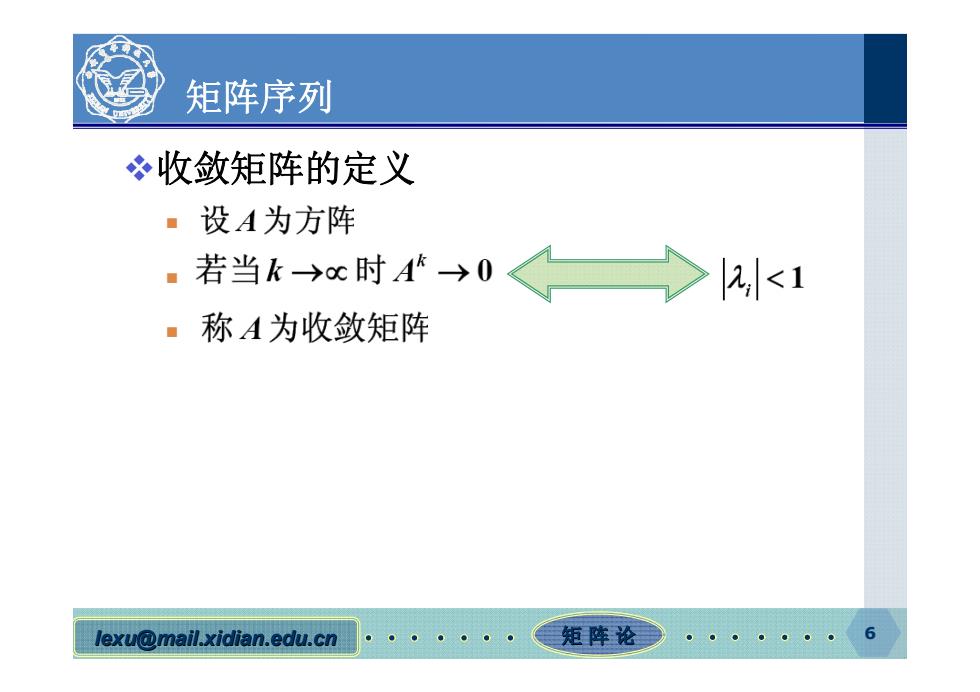
矩阵序列 冬收敛矩阵的定义 ·设A为方阵 .若当kx时A→0<>2,<1 ·称A为收敛矩阵 lexu@mail.xidian.edu.cn 矩阵论一
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 矩阵序列 收敛矩阵的定义
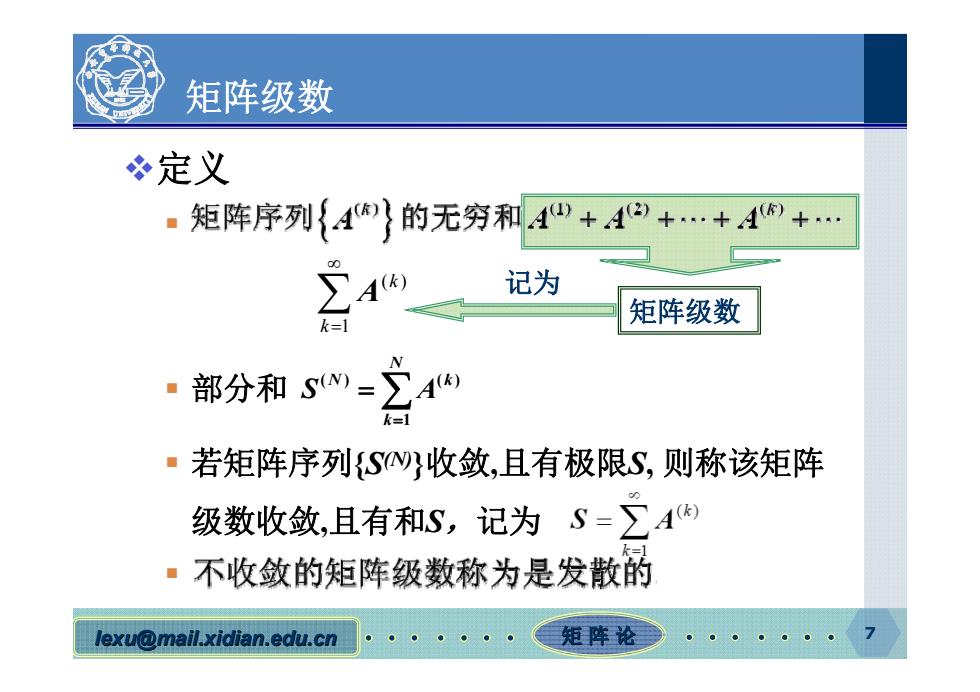
矩阵级数 必定义 ·矩阵序列{4}的无穷和4四+4+…++… 4 记为 k=1 矩阵级数 ·部分和S-2种 ■若矩阵序列{S收敛,且有极限S,则称该矩阵 级数收敛,且有和S,记为S=∑A ·不收敛的矩阵级数称为是发散的 lexu@mail.xidian.edu.cn 矩阵论雪
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 矩阵级数 定义 部分和 若矩阵序列{S(N)}收敛,且有极限S, 则称该矩阵 级数收敛,且有和S,记为 矩阵级数 1 ( ) k k A 记为 ( ) () 1 N N k k S A
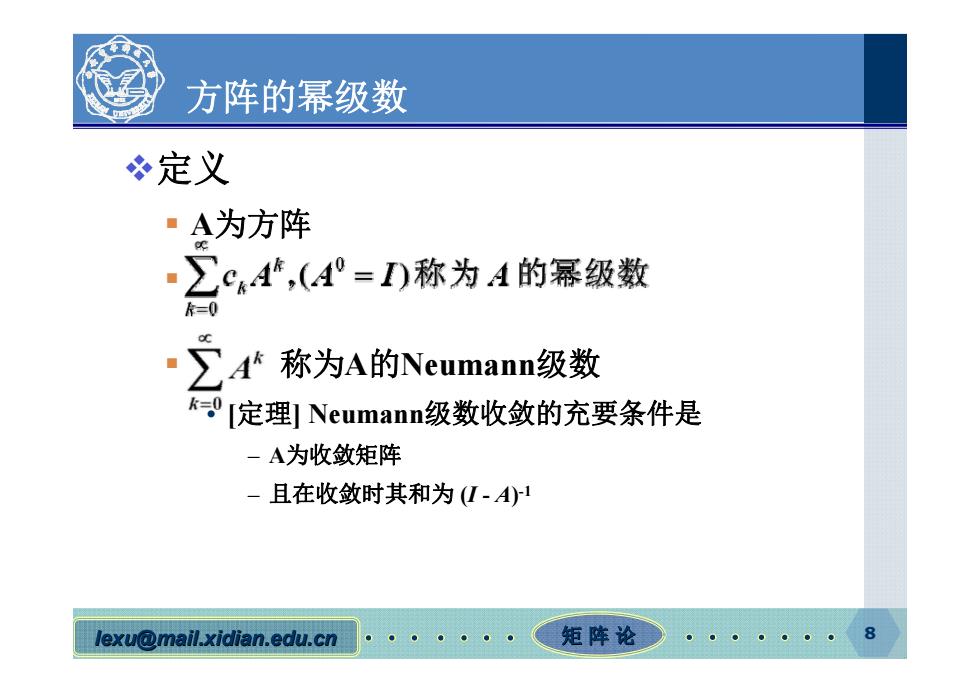
方阵的幂级数 冬定义 ·A为方阵 ·∑4,(4°=D称为1的幂级数 =0 ·∑A称为A的Neumann级数 [定理]Neumann级数收敛的充要条件是 -A为收敛矩阵 -且在收敛时其和为(I-A)1 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 方阵的幂级数 定义 A为方阵 称为A的Neumann级数 • [定理] Neumann级数收敛的充要条件是 – A为收敛矩阵 – 且在收敛时其和为 (I - A)-1

方阵的幂级数 必收敛圆 e)- ·若矩阵A的特征值全部落在幂级数的收敛圆内 则矩阵幂级数是绝对收敛的A)=∑c4,(4P=I ·反之,若A存在落在的收敛圆(z)外的特征值,则 A)是发散的 必[推论创 ·若幂级数在整个复平面上收敛,则对任何的方阵 A,(A)均收敛 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 方阵的幂级数 收敛圆 若矩阵A的特征值全部落在幂级数的收敛圆内 则矩阵幂级数是绝对收敛的 反之, 若A存在落在的收敛圆φ(z)外的特征值, 则 φ(A)是发散的 [推论] 若幂级数在整个复平面上收敛, 则对任何的方阵 A, φ(A)均收敛 0 ( ) k k k z c z 0 0 ( ) ,( ) k k k A cA A I

矩阵函数 定义 ·以矩阵为自变量的“函数”(实际上是“函矩阵”) A si血(40=分_-1) (2n+1):1 os(A0=月-1 (2n)H lexu@mail.xidian.edu.cn 矩阵论● 。。··。。。10
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 10 矩阵函数 定义 以矩阵为自变量的“函数”(实际上是“函矩阵”)