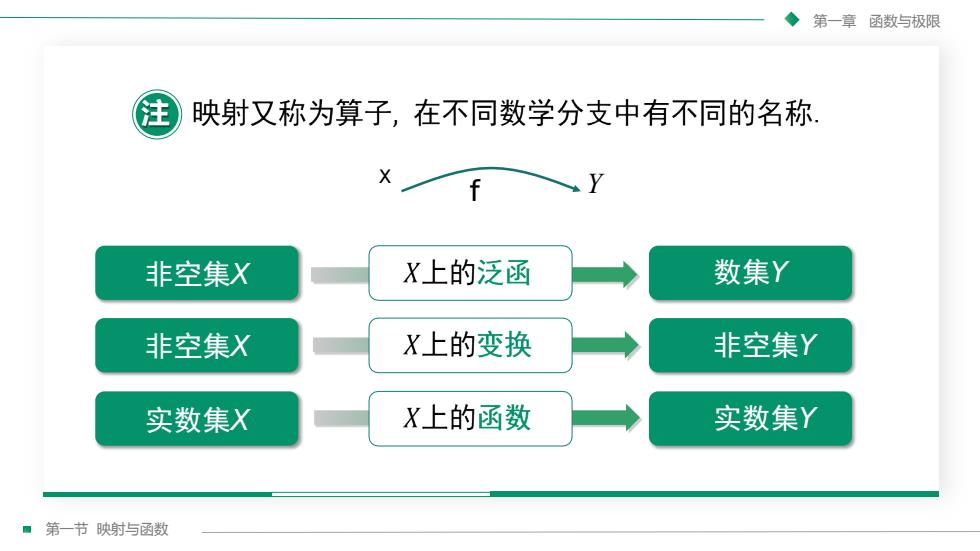
第一章函数与极限映射又称为算子,在不同数学分支中有不同的名称-XYfX上的泛函数集Y非空集XX上的变换非空集Y非空集XX上的函数实数集Y实数集X第一节映射与函数
第一节 映射与函数 第一章 函数与极限 非空集X f X Y 数集Y 非空集X 非空集Y 实数集X 实数集Y 注

第一章函数与极限2.逆映射与复合映射(1)逆映射的定义若映射f:X→Y为单射,则存在一新映射g:R,一X,使yERr,g(y)=x,其中f(x)=y,称此映射为f的逆映射定义2其定义域Df-1=Rr值域Rg-1=X记作口,此时口(=口注习惯上,记(=为Xf(X)Yy = f-1(x), x e f(X).只有单射才有逆映射,第一节映射与函数
第一节 映射与函数 第一章 函数与极限 Y X 2. 逆映射与复合映射 (1) 逆映射的定义 定义2 若映射 则存在一新映射 使 记作 其定义域 ᵰ ᵰ 其中 称此映射ᵰ ᵰ− 1 , 值域 只有单射才有逆映射. ᵰ− 1 (ᵰ) = ᵰ 为 此时ᵰ− 1 (ᵰ) = ᵰ, 注
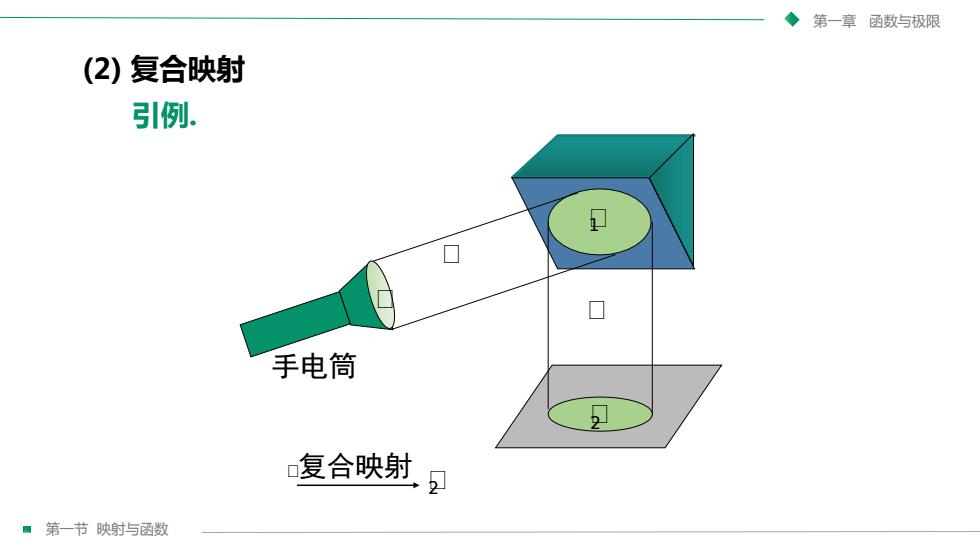
第一章函数与极限(2)复合映射引例。手电筒复合映射第一节映射与函数
第一节 映射与函数 第一章 函数与极限 (2) 复合映射 ᵰ1 ᵰ ᵰ 手电筒 ᵰ ᵰ ᵰ2 ᵰ2 复合映射 引例
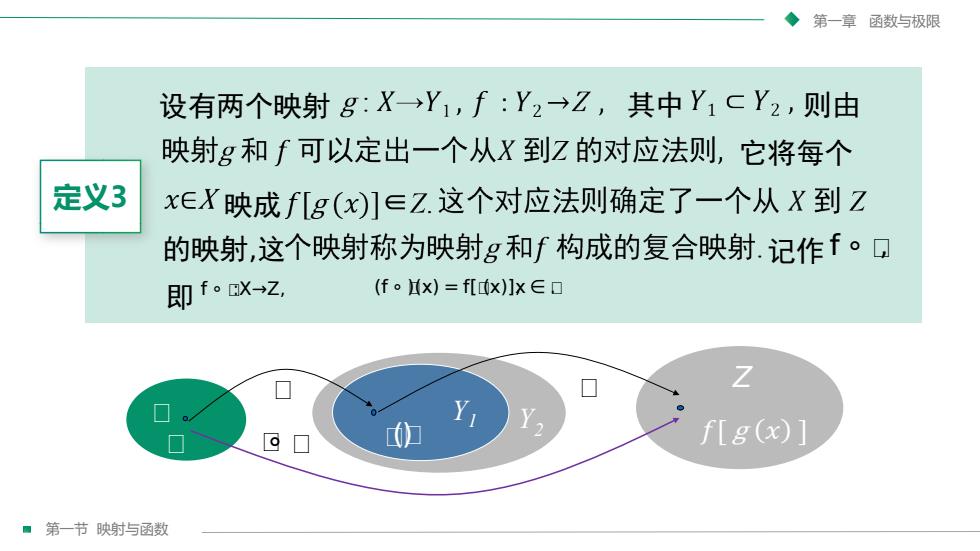
第一章函数与极限设有两个映射g:X→Yi,f:Y2→Z,其中YiCY2,则由映射g和f可以定出一个从X到Z的对应法则,它将每个定义3xEX映成f[g(x)]EZ.这个对应法则确定了一个从X到Z的映射,这个映射称为映射g和f构成的复合映射.记作f。口(f。x)=f[x)]xE即f。CX-Z,ZYi七f[g(x)]如第一节映射与函数
第一节 映射与函数 第一章 函数与极限 ᵰ 定义3 设有两个映射 其中 记作 ᵰ ᵰ ᵰ ᵰ∘ ᵰ 映成 f ∘ ᵰ, 即 则由 它将每个 ᵰ(ᵰ) 的映射,这 f ∘ ᵰ:X→Z, (f ∘ ᵰ)(x) = f[ᵰ(x)],x ∈ ᵰ. Y1 Y2 Z

第一章函数与极限注(1)映射g和f构成复合映射f。的条件:R.CDf(2映射g和f的复合是有顺序的设有映射[一1,1],对每个xER,g(x)=sinx,映射例4 - 1,1]-[0,1],对每个u E [-1,1],f(u) = V1-u2,求复合映射L9口解: Rg=[0,1]c[-1,1]=Df,并且.映射g和f构成复合映射f。日[0,1],= =f(sin x)=/1- sin?x = Icosxl第一节映射与函数
第一节 映射与函数 第一章 函数与极限 (2 ) 设有映射 对每个 映射 对每个 求复合映射 ᵰ:ᵰ→[ − 1,1], ᵰ∘ ᵰ. ᵰ:[ − 1,1]→[0,1], ᵰ∘ ᵰ(ᵰ) = ᵰ[ ᵰ(ᵰ)] ∴ f ∘ ᵰ: ᵰ→[0,1], 并且 f ∘ ᵰ的条件: 解 例4 注 (1)