
§6.3抽样分布 (2)设得到的一组样本值为1,1,2,则经验分布 函数F,c)的观察值为 0,若x<1 F3(x)={2/3,若1≤x<2 1,若x≥2 9一般,设x1,七2,xn是总体F的一个容量为n的样 本值,先将x1,x2,七n按自小到大的次序排列, 并重新编号.设为xuSx2杀.≤xm,则经验分布函 数F(x)的观察值为 0,若x<x x在x到x+1)区间 Fn(G)三k1n,若x≤x<x+n +)广x)时,由升序排 列,小于等于x的元素个 1,若x之Km 数刚好是k个 12/51
§6.3 抽样分布 (2)设得到的一组样本值为1,1,2,则经验分布 函数F3 (x)的观察值为 F3 (x)= 一般,设x1 , x2 ,., xn是总体F的一个容量为n的样 本值,先将x1 , x2 ,., xn按自小到大的次序排列, 并重新编号.设为 x(1)≤x(2)≤.≤x(n),则经验分布函 数Fn (x)的观察值为 Fn (x)= 1, 2 2 / 3, 1 2 0, 1 x x x 若 若 若 ( ) ( ) ( 1) (1) 1, / , 0, n k k x x k n x x x x x 若 若 若 x在x(k)到x(k+1)区间 (x(k+1)>x(k) )时,由升序排 列,小于等于x的元素个 数刚好是k个 12/51

§6.3抽样分布 对于经验分布函数Fmc),格里汶科(Glivenko) 在1933年证明了以下的结果 P{lim sup F(x)-F(x)=0)=1 n→o0-0<x<0 9Vx,当n→∞时经验分布函数的任一观察值 F)与总体分布函数Fx)只有微小差别,从 而在实际上可以当作Fx)来使用 。这是一种依分布收敛的性质 13/51
§6.3 抽样分布 对于经验分布函数Fn (x),格里汶科(Glivenko) 在1933年证明了以下的结果 P{ }=1 x,当n时经验分布函数的任一观察值 Fn (x)与总体分布函数F(x)只有微小差别,从 而在实际上可以当作F(x)来使用 这是一种依分布收敛的性质 lim sup | ( ) ( )| 0 Fn x F x x n 13/51

§6.3抽样分布 作为Fx)的统计量,F,c)其取值的数学期望等于Fx) 9这是因为,对于任意的x,Sx)是随机变量落在一 o到x的次数,引入随机变量X,当取值落在一o∞ 到x内时为1,否则为0,则由总体X的分布函数知 X满足0一1分布,其中X=1的概率p=Fx) ●Sx)=X1+X2+.+Xn正好满足二项分布b(n,Fx) 。于是E(Fnx)=1/nESx)=1/n(nFx)=F(x) 9可见这种估计的合理性。 14/51
§6.3 抽样分布 作为F(x)的统计量,Fn (x)其取值的数学期望等于F(x) 这是因为,对于任意的x,S(x)是随机变量落在- ∞到x的次数,引入随机变量Xi,当取值落在-∞ 到x内时为1,否则为0,则由总体X的分布函数知 Xi满足0-1分布,其中Xi=1的概率p=F(x) S(x)=X1+X2+.+Xn 正好满足二项分布b(n, F(x)) 于是E(Fn (x))=1/nE(S(x))=1/n(nF(x))=F(x) 可见这种估计的合理性。 14/51

§6.3抽样分布 统计量的分布 统计量是随机样本的函数,因此也是一个 随机变量,统计量的分布称为抽样分布, 在使用统计量进行统计推断时需要知道它 的概率分布。 。当总体分布函数已知时抽样分布是确定的, 但要求出统计量的精确分布往往是因难的。 本节介绍来自正态总体的几个常用统计量 的分布。 15/51
§6.3 抽样分布 统计量的分布 统计量是随机样本的函数,因此也是一个 随机变量,统计量的分布称为抽样分布, 在使用统计量进行统计推断时需要知道它 的概率分布。 当总体分布函数已知时抽样分布是确定的, 但要求出统计量的精确分布往往是困难的。 本节介绍来自正态总体的几个常用统计量 的分布。 15/51
§6.3抽样分布 (一)X分布 设X1,X2,Xn是来自总体N0,1)的样本,则称统计量 =X好+X3++X?服从自由度为n的2分布, 记为X~X2(n) 9自由度是指右端独立变量的个数 (n)分布的概率密度为 0.401n=1 72,y>0 0.30 n=2 027a12'e 0, 其它 0.20 n=4 =6 n=11 0.10 01234567891011121314 16/51
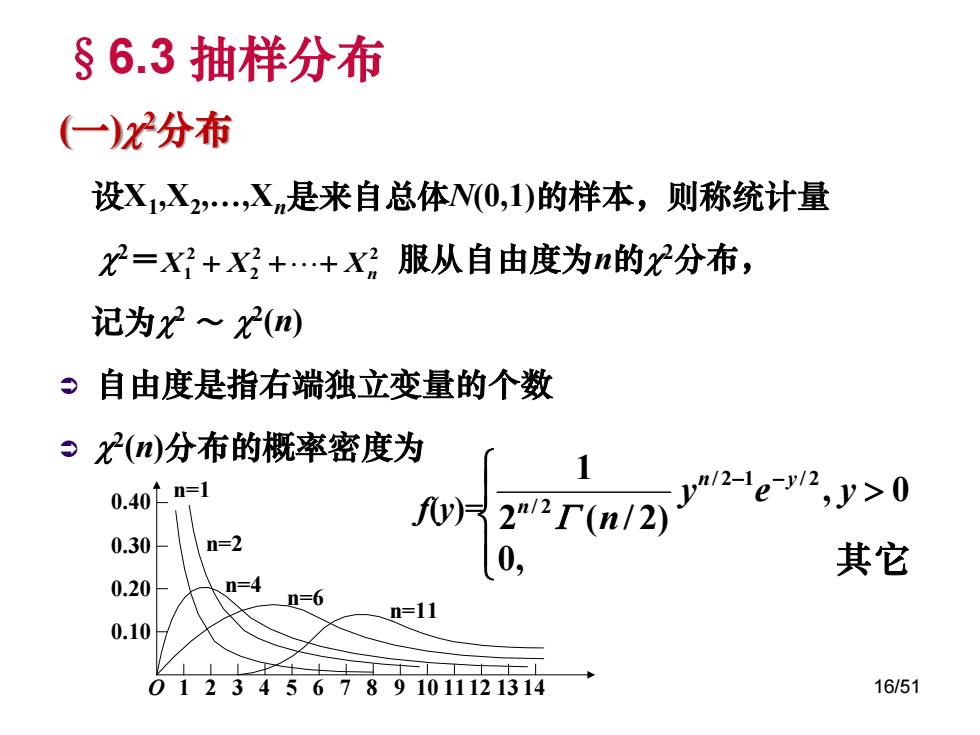
§6.3 抽样分布 (一) 2分布 设X1 ,X2 ,.,Xn是来自总体N(0,1)的样本,则称统计量 2= 服从自由度为n的 2分布, 记为 2 ~ 2 (n) 自由度是指右端独立变量的个数 2 (n)分布的概率密度为 f(y)= 2 2 2 2 X1 X Xn 0, 其 它 , 0 2 ( / 2) 1 / 2 1 / 2 / 2 y e y n n y n O 1 2 3 4 5 6 7 8 9 10 1112 13 14 0.10 0.20 0.30 0.40 n=1 n=2 n=4 n=6 n=11 16/51