
知识点回顾第一章 随机现象 统计规律性 随机试验 1.相同条件下可重复进行; 2.每次试验可能结果不止一个,但可以预知所有可能结果; 3.每次试验前不能预知哪一个结果出现 样本空间 (映射) 随机变量 (取值) →总体 S X N (最基本的概念) (单值实值函数) (取自X的全部可能试验观察值) 随机事件 随机事件 部分个体 (子集,S,基本事件) (子集) (简单随机样本) 概率空间(样本空间S,事件域F,事件的概率P) 关系:包含,相等,和事件,积事件,差事件,互不相容,逆事件(对立事件) 事件间的关 系和运算 描述:元素考察法;韦恩图法 运算:交换律;结合律;分配律;德摩根律
知识点回顾-第一章 随机现象 统计规律性 随机试验 1.相同条件下可重复进行; 2.每次试验可能结果不止一个,但可以预知所有可能结果; 3.每次试验前不能预知哪一个结果出现 样本空间 S 随机变量 X 总体 N (最基本的概念) (单值实值函数) (取自X的全部可能试验观察值) 随机事件 (子集,f,S,基本事件) 随机事件 (子集) 部分个体 (简单随机样本) 事件间的关 系和运算 关系:包含,相等,和事件,积事件,差事件,互不相容,逆事件(对立事件) 描述:元素考察法;韦恩图法 运算:交换律;结合律;分配律;德·摩根律 (映射) (取值) 概率空间(样本空间S, 事件域F, 事件的概率P)
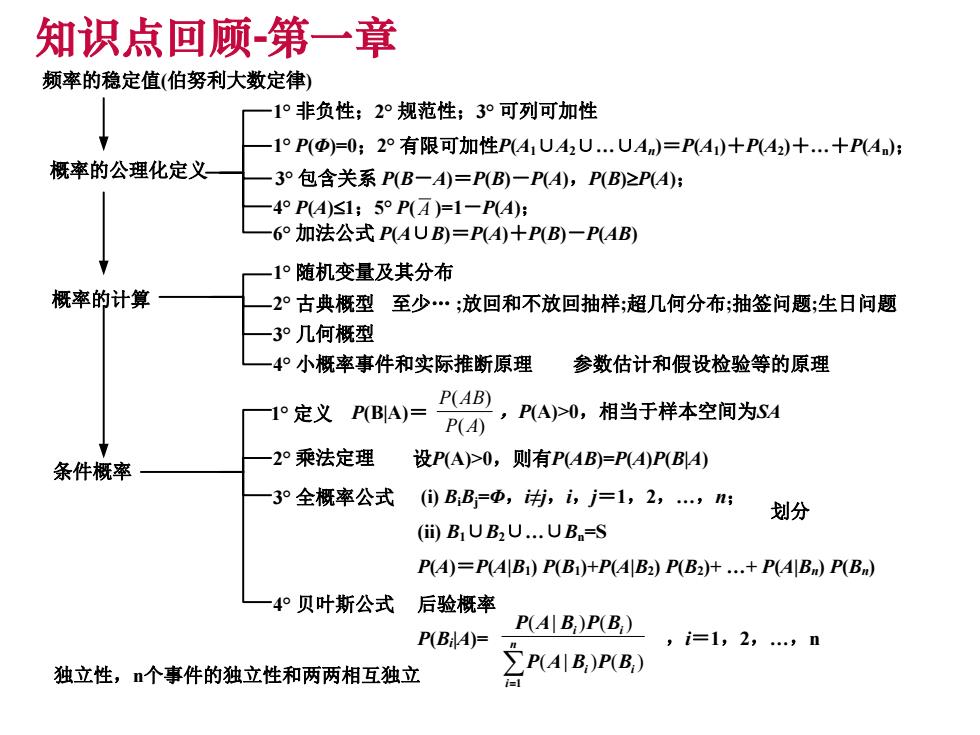
知识点回顾-第一章 频率的稳定值(伯努利大数定律) 1°非负性;2°规范性;3°可列可加性 -1°P()=0;2°有限可加性PA1UA2U.UAn)=PA1)+PA2)+.十PA); 概率的公理化定义 3°包含关系P(B-A)=P(B)-P(A),P(B)2P4): 4°P40s1;5°P(A)=1-P4A): 6°加法公式P(AUB)=P(十P(B)一P(AB) -1°随机变量及其分布 概率的计算 -2°古典概型至少.;放回和不放回抽样;超几何分布;抽签问题;生日问题 -3°几何概型 -4°小概率事件和实际推断原理参数估计和假设检验等的原理 TP定义ABA=,AA0,相当于样本空间为4 一2°乘法定理 条件概率 设P(A)>0,则有PAB)=P(A)P(B4) 3°全概率公式 (①BB=中,i,j=1,2,n; 划分 (ii)B1UB2 U.UB=S P(A)=P(A B1)P(B1)+P(A B2)P(B2)+.+P(A B)P(B) 4°贝叶斯公式后验概率 P(AB)P(B) P(BiA)= ,i=1,2,n 独立性,个事件的独立性和两两相互独立 P(AIB)P(B)
知识点回顾-第一章 概率的公理化定义 频率的稳定值(伯努利大数定律) 概率的计算 1°非负性;2°规范性;3°可列可加性 1°P(Φ)=0;2°有限可加性P(A1∪A2∪.∪An)=P(A1)+P(A2)+.+P(An); 3°包含关系 P(B-A)=P(B)-P(A),P(B)³P(A); 4°P(A)£1;5°P( )=1-P(A); 6°加法公式 P(A∪B)=P(A)+P(B)-P(AB) A 1°随机变量及其分布 2°古典概型 至少. ;放回和不放回抽样;超几何分布;抽签问题;生日问题 4°小概率事件和实际推断原理 参数估计和假设检验等的原理 条件概率 1°定义 P(B|A)= ( ) ( ) P A P AB ,P(A)>0,相当于样本空间为SA 2°乘法定理 设P(A)>0,则有P(AB)=P(A)P(B|A) 3°全概率公式 (i) BiBj=Φ,i≠j,i,j=1,2,.,n; (ii) B1∪B2∪.∪Bn=S 划分 P(A)=P(A|B1) P(B1)+P(A|B2) P(B2)+ .+ P(A|Bn) P(Bn) 4°贝叶斯公式 后验概率 P(Bi|A)= ,i=1,2,.,n n i i i i i P A B P B P A B P B 1 ( | ) ( ) ( | ) ( ) 独立性,n个事件的独立性和两两相互独立 3°几何概型
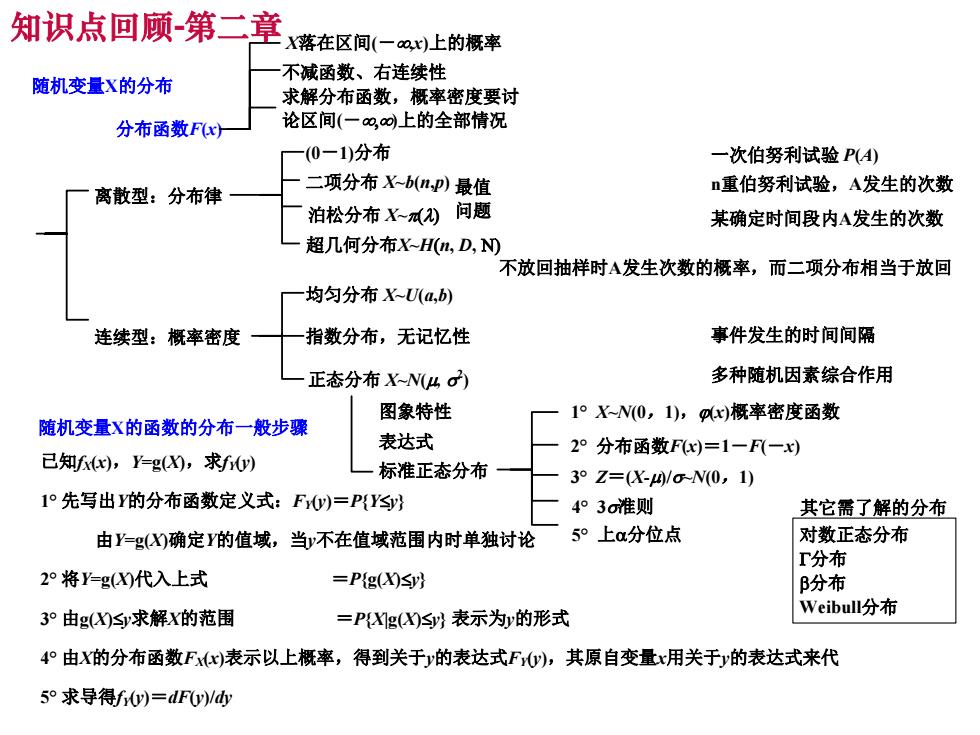
知识点回顾-第二章 X落在区间(一o,x)上的概率 不减函数、右连续性 随机变量X的分布 求解分布函数,概率密度要讨 分布函数Fx 论区间(一o∞,上的全部情况 -(0-1)分布 一次伯努利试验P(4) 离散型:分布律 二项分布X~b(np)最值 n重伯努利试验,A发生的次数 泊松分布X)问题 某确定时间段内A发生的次数 超几何分布X~H,D,) 不放回抽样时A发生次数的概率,而二项分布相当于放回 均匀分布XU(a,b) 连续型:概率密度 指数分布,无记忆性 事件发生的时间间隔 正态分布X-N(4d) 多种随机因素综合作用 图象特性 1°X-N(0,1),gx)概率密度函数 随机变量X的函数的分布一般步骤 表达式 2°分布函数Fx)=1一F(一x) 已知c),Y=g(X),求fy) 标准正态分布 3°Z=(X-/cN0,1) 1°先写出Y的分布函数定义式:F)=P{Y} 4°3o准则 其它需了解的分布 由Y=g)确定Y的值域,当不在值域范围内时单独讨论 5°上分位点 对数正态分布 分布 2°将Y=g(X代入上式 =P(g(X)S) 分布 3°由g(X)S求解X的范围 =Pg()sy表示为y的形式 Weibull分布 4°由X的分布函数Fxx)表示以上概率,得到关于y的表达式Fy),其原自变量x用关于y的表达式来代 5°求导得fy)=dFy)/
随机变量X的分布 分布函数F(x) 离散型:分布律 连续型:概率密度 (0-1)分布 二项分布 X~b(n,p) 泊松分布 X~p(l) 最值 问题 均匀分布 X~U(a,b) 指数分布,无记忆性 正态分布 X~N(m, s 2 ) 图象特性 表达式 标准正态分布 1° X~N(0,1),j(x)概率密度函数 2° 分布函数F(x)=1-F(-x) 3° Z=(X-m)/s~N(0,1) 4° 3s准则 5° 上a分位点 X落在区间(-,x)上的概率 不减函数、右连续性 求解分布函数,概率密度要讨 论区间(-,)上的全部情况 随机变量X的函数的分布一般步骤 已知fX(x),Y=g(X),求fY(y) 1°先写出Y的分布函数定义式:FY(y)=P{Y£y} 由Y=g(X)确定Y的值域,当y不在值域范围内时单独讨论 2°将Y=g(X)代入上式 =P{g(X)£y} 3°由g(X)£y求解X的范围 =P{X|g(X)£y} 表示为y的形式 4°由X的分布函数FX(x)表示以上概率,得到关于y的表达式FY(y),其原自变量x用关于y的表达式来代 5°求导得fY(y)=dF(y)/dy 一次伯努利试验 P(A) n重伯努利试验,A发生的次数 某确定时间段内A发生的次数 事件发生的时间间隔 多种随机因素综合作用 其它需了解的分布 对数正态分布 G分布 b分布 Weibull分布 超几何分布X~H(n, D, N) 不放回抽样时A发生次数的概率,而二项分布相当于放回 知识点回顾-第二章

知识点回顾第三章 二维随机变量(区,):X=X,Y-Y{.X和Y之间存在相互关系 二维随机变量区,)的分布主要讨论四种关系 1°作为整体的联合分布 X和Y的联合分布函数) X和Y的联合分布律 凡wyW-PX≤, P=xY=y州=P防,ij户1,2,. F(x,y)=∑∑Pg 所有的分布律 xy不减函数、右连续性 ,≤ry, 和概率密度共 X和Y的联合概率密度c) 有的性质:非 O<Fx,y)s1 负性、规范性 落在矩形区域的橘率 F(x.y)=f(u.v)dudy 一2°整体与分量的关系,边缘分布 X的边缘分布律p: X的边缘分布函数Fx=凡,网 Y的边缘分布律P Y的边缘分布函数F=凡oy) X的边缘概率密度) fx()=[f(x.y)dy Y的边缘概率密度∫) f(y)=[f(x,y)dx 一3°X,Y之间的条件关系,条件分布 条件分布律 条件概率密度 作为条件的概率不为0时或者y的取值范围 三要素 条件概率的表达式:联合/边缘 定义域或x范围
知识点回顾-第三章 二维随机变量 (X,Y): X=X{e}, Y=Y{e}. X和Y之间存在相互关系 二维随机变量(X,Y)的分布主要讨论四种关系 1 作为整体的联合分布 3 X,Y之间的条件关系,条件分布 所有的分布律 和概率密度共 有的性质:非 负性、规范性 2 整体与分量的关系,边缘分布 X和Y的联合分布函数F(x,y) F(x,y)=P{X£x,Y£y} x,y不减函数、右连续性 0£F(x,y)£1 落在矩形区域的概率 X和Y的联合分布律 P{X=xi , Y=yj}=pij , i, j=1,2, . £ £ x x y y ij i j F(x, y) p X和Y的联合概率密度 f(x,y) y x F(x, y) f (u,v)dudv X的边缘分布函数FX(x)=F(x,) Y的边缘分布函数FY(y)=F(,y) X的边缘分布律 pi· Y的边缘分布律 p·j X的边缘概率密度fX(x) Y的边缘概率密度fY(y) f x f x y dy X ( ) ( , ) f y f x y dx Y ( ) ( , ) 条件分布律 条件概率密度 三要素 作为条件的概率不为0时j或者y的取值范围 条件概率的表达式:联合/边缘 定义域i或x范围

第三章多维随机变量及其分布 9§3.1二维随机变量 9§3.2边缘分布 9§3.3条件分布 。§3.4相互独立的随机变量 9§3.5两个随机变量的函数的分布
第三章 多维随机变量及其分布 §3.1 二维随机变量 §3.2 边缘分布 §3.3 条件分布 §3.4 相互独立的随机变量 §3.5 两个随机变量的函数的分布