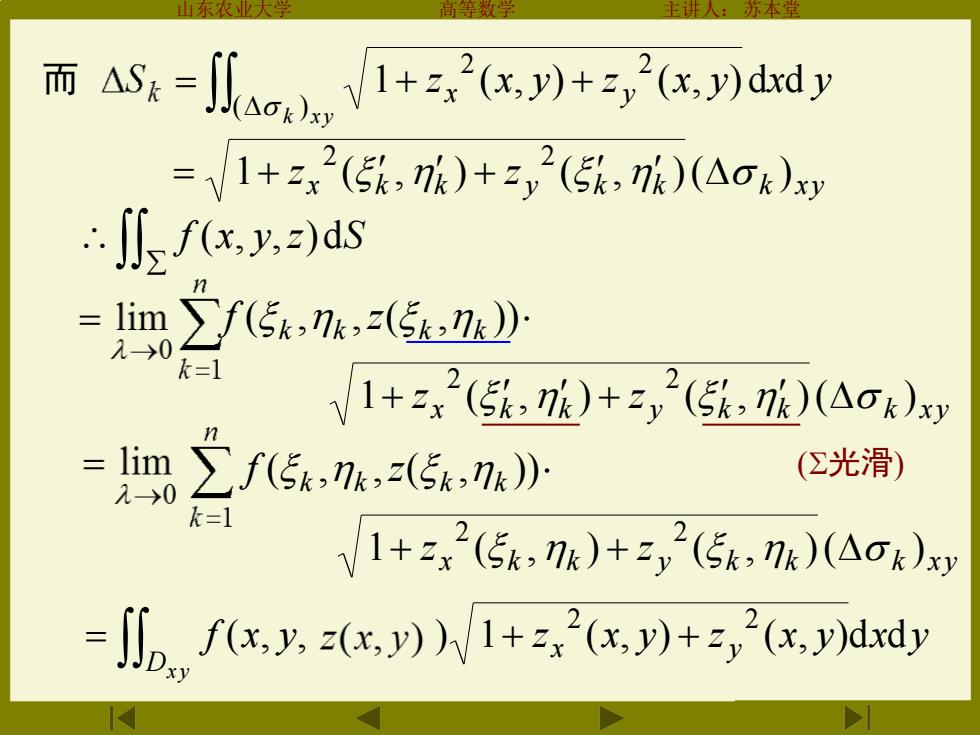
而△S=any1+,2(x,川+dd =1+2x2(5,7k)+zy2(5,k)(Aok)xy “J八fx,y,2)ds =2f5%,2》 k=1 V1+2x2(5k,)+2y2(5k,)(△ok)xy =]im∑f(5k,k,2(5,x)》 (光滑) k=1 √1+2x2(5,x)+3y2(5k,7k)(△ok)xy f(x,y.z(.y))+2(x)+,2(x.y)dxdy
山东农业大学 高等数学 主讲人:苏本堂 z x y z x y x y k x y x y 1 ( , ) ( , ) d d ( ) 2 2 + + x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 = + + x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 + + x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 + + f x y z x y z x y x y x y Dx y ( , , ) 1 ( , ) ( , )d d 2 2 = + + ( , , ( , )) k k k k f z ( , , ( , )) k k k k f z f (x, y,z)dS 而 (光滑)

山东农业大 化曲面积分为二重积分 设曲面Σ的方程为z=z(x,y),∑在xOy面上的投影区域 为D函数z=z(x,y)在D上具有连续偏导数,被积函数x, y,)在∑上连续,则 小fx,yaS=∬fxy2(x川W1+x+x,). 讨论: 如果积分曲面Σ由方程yW2,x)给出或由x=x0y,2)给 出,那么孔x,y,z)在∑上对面积的曲线面积分如何计算? 提示: 对于2:y=(2,x),有 小fxy,2S=J∬fIx,(2,x,zV1+y2,x)+y2(2,x)dd
山东农业大学 高等数学 主讲人:苏本堂 = + + Dzx z x f (x, y,z)dS f[x, y(z, x),z] 1 y (z, x) y (z,x)dzdx 2 2 化曲面积分为二重积分 设曲面的方程为z=z(x y) 在xOy面上的投影区域 为Dxy 函数z=z(x y)在Dxy上具有连续偏导数被积函数f(x y z)在上连续 则 = + + Dx y x y f (x, y,z)dS f[x, y,z(x, y)] 1 z (x, y) z (x, y)dxdy 2 2 讨论 如果积分曲面由方程y=y(z x)给出或由x=x(y z)给 出 那么 f(x y z)在上对面积的曲线面积分如何计算? 提示 对于 y=y(z x) 有