
复变函数第二节复数的几何表示一、复平面二、复球面三、小结与思考u
第二节 复数的几何表示 一、复平面 二、复球面 三、小结与思考
复变函数一、复平面1.复平面的定义复数z=x+i与有序实数对(x,y)成一一对应.因此,一个建立了直角坐标的平面可以用来表示复数,通常把横轴叫实轴或x轴,纵轴叫虚轴或√轴.这种用来表示复数的平面叫复平面.yz=x+iy1(x,y)复数z=x+i可以用复平面上的点(x,)表示+xX0u
2 一、复平面 1. 复平面的定义 . . , , . , ( , ) 面 叫虚轴或 轴 这种用来表示复数的平面叫复平 用来表示复数 通常把横轴叫实轴或 轴 纵 轴 对 应 因 此 一个建立了直角坐标系的平面可以 复 数 与有序实数对 成一一 y x z = x + iy x y 面上的点( , )表示. 复数 可以用复平 x y z = x + iy (x, y) x y x y o z = x + iy

复变函数2.复数的模(或绝对值)复数z=x+i可以用复平面上的向量OP表示向量的长度称为的模或绝对值义记为z=r=/x2+y2.Pz=x+iy1显然下列各式成立+xx0[≤,x≤z,z·z==z2z≤x+yu
3 2. 复数的模(或绝对值) 向量的长度称为z的模或绝对值, 复数 z = x + iy 可以用复平面上的向量OP 表示, . 2 2 记为 z = r = x + y x y x y o z = x + iy P 显然下列各式成立 r x z, y z, z x + y , . 2 2 zz = z = z

复变函数3.复数的辐角在z≠0的情况下,以正实轴为始边以表示z的向量OP为终边的角的弧度数0称为z的辐角记作 Argz=θ.说明任何一个复数z≠0有无穷多个辐角那么z的全部辐角为如果θ 是其中一个辐角Argz=,+2k元(k为任意整数)特殊地,当z=0时,z=0,辐角不确定u
4 3. 复数的辐角 Arg . , 0 , , = z z OP z z 记 作 的向量 为终边的角的弧度数 称 为 的辐角 在 的情况下 以正实轴为始边 以表示 说明 任何一个复数 z 0有无穷多个辐角, , 如果1 是其中一个辐角 Arg 2 π ( ). z = 1 + k k为任意整数 特殊地, 当 z = 0时, z = 0, 那么z的全部辐角为 辐角不确定
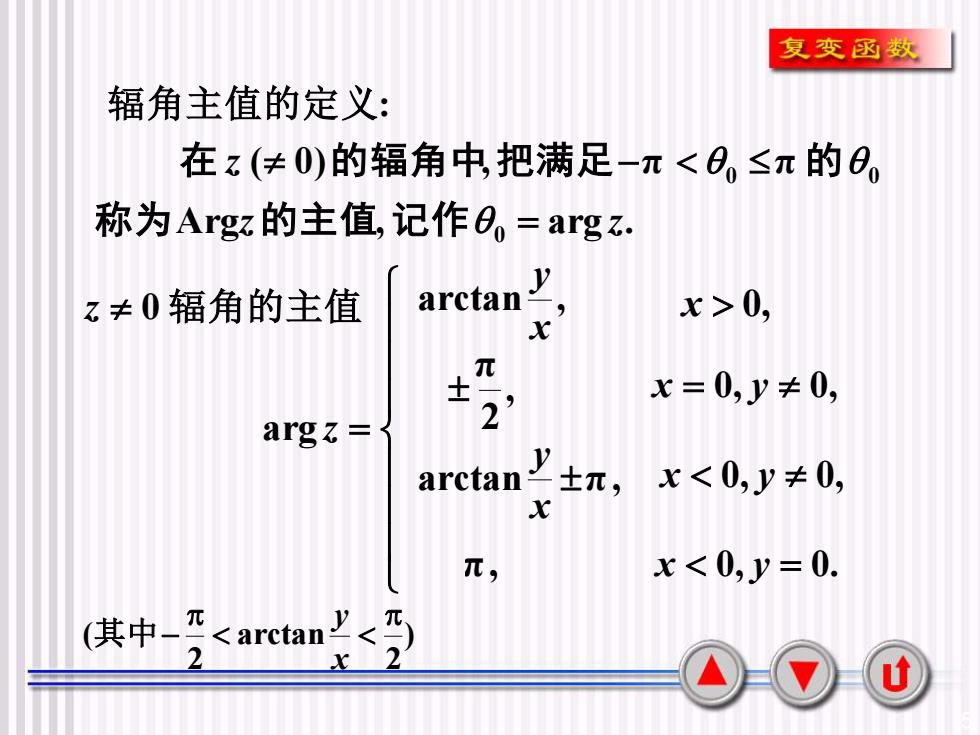
复变函数辐角主值的定义:在(0)的辐角中,把满足一元<≤元的0称为Argz的主值,记作。=argz.Varctanx >0,z≠0辐角的主值x元x = 0,y 0,2argz =3yx< 0,y± 0,±元,arctanxx<0,y= 0.元,元V元(其中.2arctan2XU
5 辐角主值的定义: Arg , arg . ( 0) , π π 0 0 0 z z z = − 称 为 的主值 记 作 在 的辐角中 把满足 的 x 0, ) 2 arctan 2 ( − x y 其中 z 0 辐角的主值 arg z = x = 0, y 0, x 0, y 0, x 0, y = 0. arctan , x y , 2 π arctan π, x y π