
复变函数第一章复数与复变函数一、重点与难点二、 内容提要三、典型例题U

复变函数一、重点与难点重点:1.复数运算和各种表示法2.复变函数以及映射的概念难点:1.复数方程表示曲线以及不等式表示区域2.映射的概念拉
2 一、重点与难点 重点: 难点: 1. 复数运算和各种表示法 2. 复变函数以及映射的概念 1. 复数方程表示曲线以及不等式表示区域 2. 映射的概念
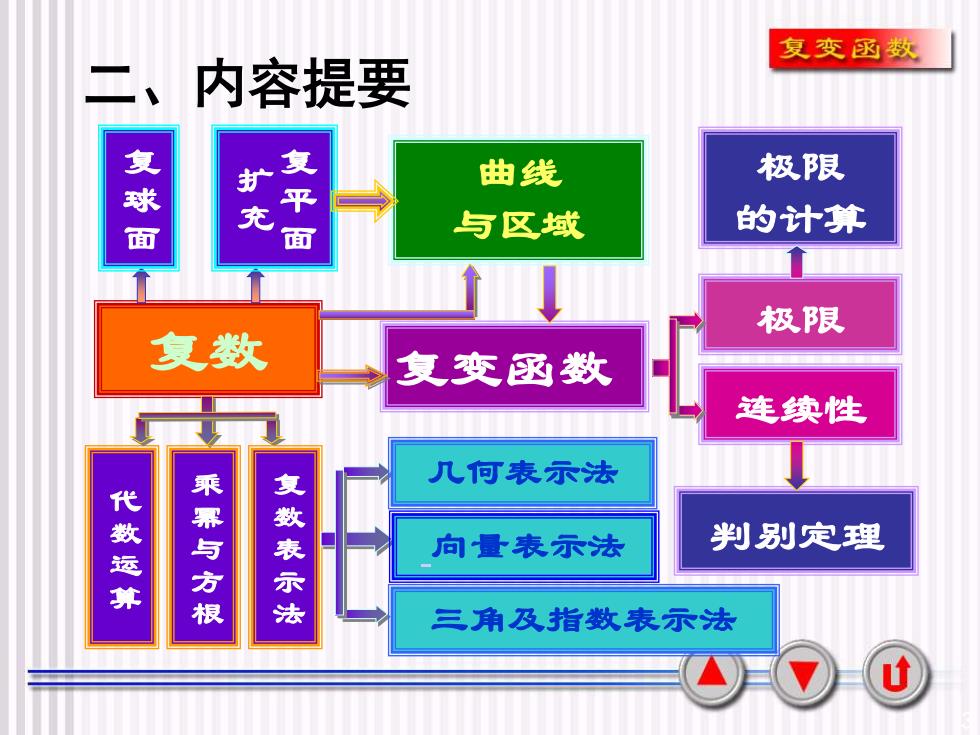
复变函数二、内容提要复球面复平面极限曲线扩充的计算与区域极限复数复变函数连续性几何表示法乘幂与方根复数表示法代数运算判别定理向量表示法三角及指数表示法u
3 二、内容提要 复数 复变函数 极限 连续性 代 数 运 算 乘 幂 与 方 根 复 数 表 示 法 几何表示法 向量表示法 三角及指数表示法 复 球 面 复 平 面 扩 充 曲线 与区域 判别定理 极限 的计算

复变函数1.复数的概念对于任意两实数x,y,我们称z=x+yi或z=x+i为复数其中x,分别称为z的实部和虚部记作 x = Re(z), =Im(z)当x=0,≠0时,z=iy称为纯虚数当y=0时,z=x+0i,我们把它看作实数x当x=0,y=0时,z=0U
4 1.复数的概念 . , , 或 为复数 对于任意两实数 我们称 z x iy x y z x yi = + = + 其 中x, y 分别称为z的实部和虚部, 记 作 x = Re(z), y = Im(z). 当 x = 0, y 0时, z = iy 称为纯虚数; 当 y = 0时, z = x + 0i,我们把它看作实数x. 当 x = 0, y = 0时, z = 0

复变函数2.复数的代数运算设两复数=+i,=+i2,1)两复数的和zi ± z2 =(xi ±x2)+i(yi± y2)2)两复数的积Z1 :Z2 = (xix2 - yiy2) +i(x2yi +Xiy2)3)两复数的商Zi - XiX2 + yiy2+ix2i-Xiy222Z.2X2+ y2X2+ y2u
5 , , 1 1 1 2 2 2 设两复数 z = x + iy z = x + iy 1) 两复数的和 ( ) ( ). 1 2 1 2 1 2 z z = x x + i y y 2) 两复数的积 ( ) ( ). 1 2 1 2 1 2 2 1 1 2 z z = x x − y y + i x y + x y 3)两复数的商 . 2 2 2 2 2 1 1 2 2 2 2 2 1 2 1 2 2 1 x y x y x y i x y x x y y z z + − + + + = 2. 复数的代数运算