
当-1≤x≤1时, (注意积分限的确定方法) D fx (x)=f(x,y)dy -0d ++0a 熟练时,被积函数为零的部分可以不写
当-1≤x≤1时, 1 . 2 0 1 0 ( ) ( , ) 2 1 1 1 1 2 2 2 2 x d y d y d y f x f x y d y x x x x X = − + + = = − − − − − − − − ( 注意积分限的确定方法 ) 熟练时,被积函数为零的部分可以不写

故的 x廷[-1,1]; 由X和Y在问题中地位的对称性,将上式中 的x改为y,得到Y的边缘概率密度 f() 2-,ye-1n = y年[-1,1] @回的
由X 和Y 在问题中地位的对称性, 将上式中 的 x 改为 y,得到 Y 的边缘概率密度 − − − = 0, [ 1,1]; 1 , [ 1,1], 2 ( ) 2 x x x 故 f X x − − − = 0, [ 1,1]. 1 , [ 1,1], 2 ( ) 2 y y y f y Y

例5:设XY)的概率密度为 cy(2-x),0≤x≤1,0≤y≤x, f(x,y)= 0 其他 求(1).c的值;(2).边缘密度。 解:(I).fx,y) =92- =c[x(2-x)/2]k 0 = 5c/24=1, 之℃=24/5; @@网
例5:设(X, Y)的概率密度为 − = 0 , . (2 ), 0 1, 0 , ( , ) 其他 cy x x y x f x y 求 (1). c的值; (2). 边缘密度。 = 5c/24=1, c = 24/5; cy x dy dx x (2 ) 1 0 0 = − − − 解: (1). f (x, y)dxdy c [x (2 x)/ 2] dx 1 0 2 = −

解:(2) 注意积分限 V=X x-了号2-x海 0 -号x0- 。0≤x≤1, 注意取值范围 容四
解: (2) = − x f X x y x dy 0 (2 ) 5 24 ( ) (2 ), 5 12 2 = x − x 0 x 1, 注意积分限 注意取值范围
注意积分限 V=X -0-h -房2分0ss1 注意取值范围
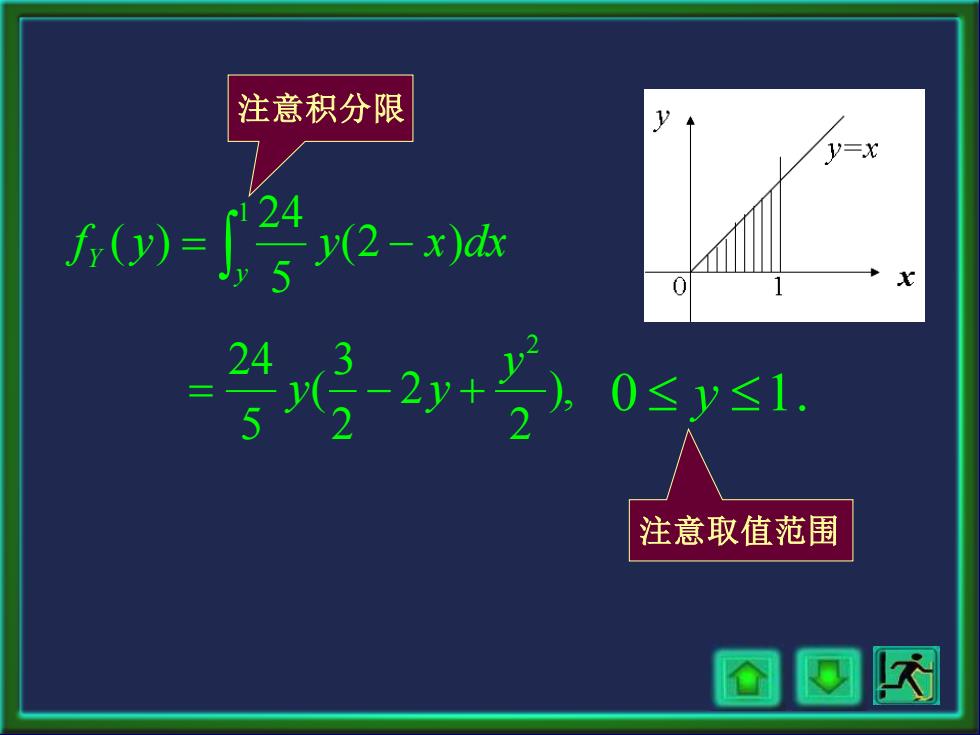
), 2 2 2 3 ( 5 24 2 y = y − y + = − 1 (2 ) 5 24 ( ) y f Y y y x dx 0 y 1. 注意积分限 注意取值范围