
§4.2方差 前面介绍了随机变量的数学期望。数 学体现了随机变量取值的平均水平,是随 机变量的重要的数字特征。 但在一些场合,仅仅知道平均值是不够 的,还需了解其他数字特征
前面介绍了随机变量的数学期望。数 学体现了随机变量取值的平均水平,是随 机变量的重要的数字特征。 但在一些场合,仅仅知道平均值是不够 的,还需了解其他数字特征。 §4.2 方差
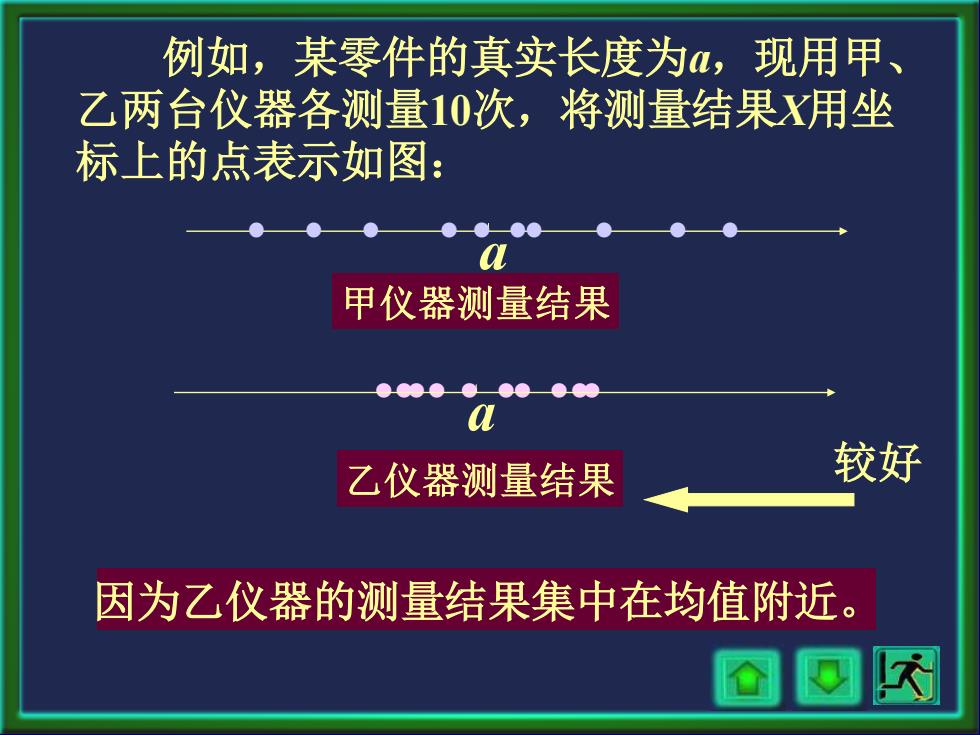
例如,某零件的真实长度为α,现用甲、 乙两台仪器各测量10次,将测量结果X用坐 标上的点表示如图: 甲仪器测量结果 乙仪器测量结果 较好 因为乙仪器的测量结果集中在均值附近
例如,某零件的真实长度为a,现用甲、 乙两台仪器各测量10次,将测量结果X用坐 标上的点表示如图: a •••• • •• ••• 乙仪器测量结果 a • • • • • •• • • • 甲仪器测量结果 较好 因为乙仪器的测量结果集中在均值附近
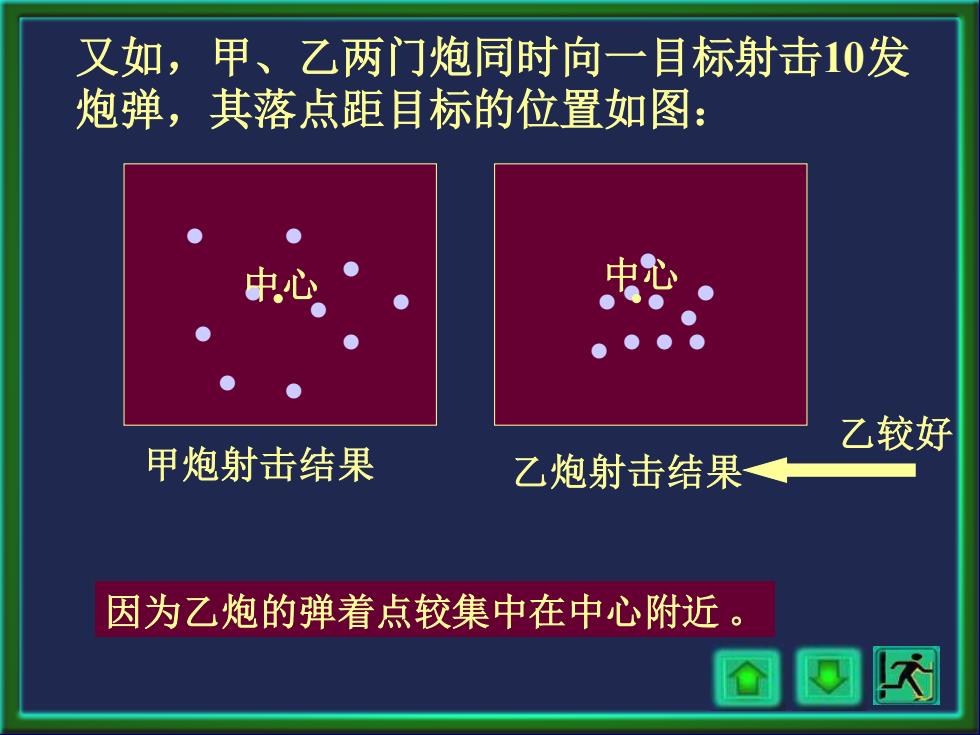
又如,甲、乙两门炮同时向一目标射击10发 炮弹,其落点距目标的位置如图: 乙较好 甲炮射击结果 乙炮射击结果 因为乙炮的弹着点较集中在中心附近
又如,甲、乙两门炮同时向一目标射击10发 炮弹,其落点距目标的位置如图: 甲炮射击结果 乙炮射击结果 乙较好 因为乙炮的弹着点较集中在中心附近 。 • • • • • • • • • • • • • • • • • • • • 中心 中心

为此需要引进另一个数字特征,用它来 度量随机变量取值偏离其中心(均值)的程度。 这个数字特征就是我们要介绍的方差
为此需要引进另一个数字特征,用它来 度量随机变量取值偏离其中心(均值)的程度。 这个数字特征就是我们要介绍的方差

4.2.1方差的定义 采用平方是为了保证一切 差值X-EX)都起正的作用 定义1:设X是一随机变量,若EX-EX)P 存在,则称其为X的方差,记成Var),即 Var(X)=E[X-E(X)2; 并称Wa(X)为X的标准差。 注:有的书上也将Var记成D)
4.2.1 方差的定义 注: 有的书上也将Var(X)记成D(X)。 定义1: 设X 是一随机变量,若E[X-E(X)]2 存在, 则称其为X 的方差,记成Var(X),即 Var(X)= E[X-E(X)]2 ; (1) 并称 Var(X) 为X的标准差。 采用平方是为了保证一切 差值[X-E(X)]都起正的作用