
第三章随机向量 有些随机现象只用一个随机变量来描述是 不够的,需要用几个随机变量来同时描述。 例如: 1.某人体检数据 血压X和心律Y; 2.钢的基本指标 含碳量X,含硫量和 硬度Z; 3.导弹在空中位置一 坐标X,Y,Z
第三章 随机向量 有些随机现象只用一个随机变量来描述是 不够的,需要用几个随机变量来同时描述。 3. 导弹在空中位置——坐标(X, Y, Z)。 1. 某人体检数据——血压X和心律Y; 例如: 2. 钢的基本指标——含碳量X,含硫量 Y和 硬度 Z ;

般地,将随机试验涉及到的个随机 量X,X,X放在一起,记成(X,X, X),称n维随机向量(或变量)。 由于从二维随机向量推广到多维随机向 量并无实质性困难,所以,我们着重讨论二 维随机向量
一般地, 将随机试验涉及到的 n 个随机 量 X1, X2 , ., Xn 放在一起,记成(X1, X2 , ., Xn ),称 n 维随机向量(或变量)。 由于从二维随机向量推广到多维随机向 量并无实质性困难,所以,我们着重讨论二 维随机向量

§3.1二维随机向量及其分布函数 设试验E的样本空间为2,X=X(O)与Y= Y(o)是定义在2上的两个随机变量,由它们构 成的向量(X,)称为二维随机向量。 二维随机向量X,)的性质不仅与X和Y 的性质有关,而且还依赖于和Y之间的相互 关系。因此,必须把X,)作为一个整体来看 待,加以研究。 为此,首先引入二维随机向量X,)的分 布函数的概念
§3.1 二维随机向量及其分布函数 设试验E的样本空间为Ω,X=X()与Y= Y()是定义在Ω上的两个随机变量, 由它们构 成的向量 (X, Y) 称为二维随机向量。 二维随机向量(X, Y)的性质不仅与X 和Y 的性质有关,而且还依赖于X和Y之间的相互 关系。因此,必须把(X, Y)作为一个整体来看 待,加以研究。 为此,首先引入二维随机向量(X, Y)的分 布函数的概念

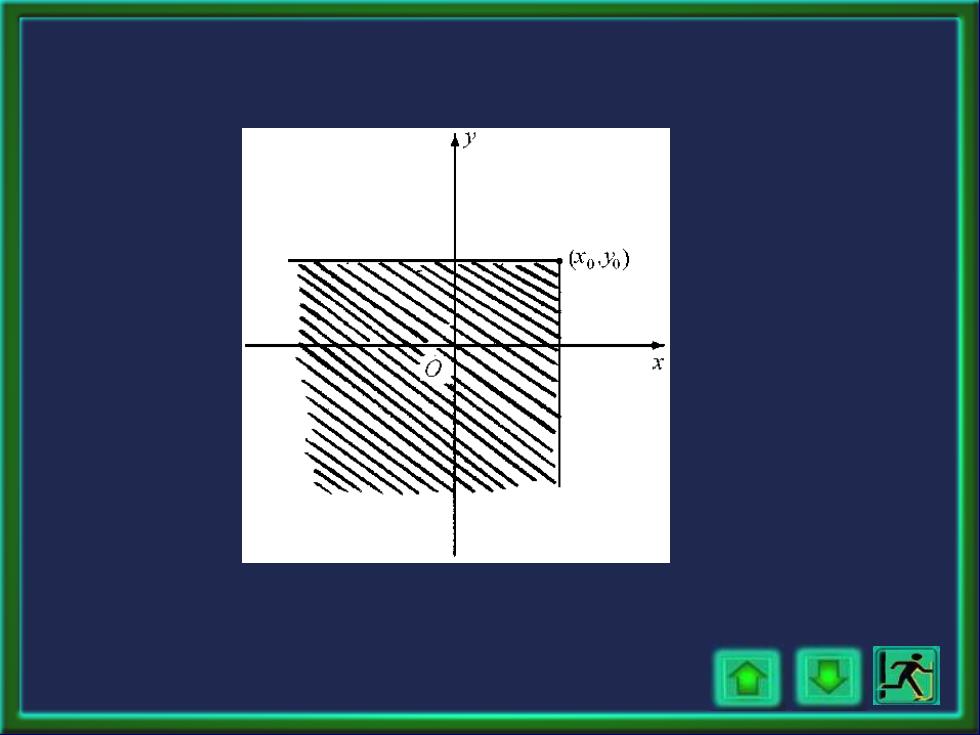
定义二维随机向量X,)的联合分布函数为 F(x,y)=P(X≤x,Y≤y), 一o0<X≤0 一0≤y<0. 如果将X,Y)看成平面上随机点的坐标。 取定xo,yo∈R=(-o,o),F(xo,Jyo)就是点(X,Y) 落在平面上,以(xoy)为顶点,且位于该点 左下方无限矩形区域上的概率
定义二维随机向量(X, Y) 的联合分布函数为 , . ( , ) ( , ), − − = x y F x y P X x Y y 取定x0,y0R=(-∞,∞), F(x0,y0)就是点(X,Y) 落在平面上,以(x0,y0)为顶点,且位于该点 左下方无限矩形区域上的概率。 如果将 (X, Y) 看成平面上随机点的坐标
(0%) @@的