
例2:(打开书P59) 求例3.2.2中(X,)的分量 X和Y的边缘分布。 解:PX=0}=PX=0,Y=-0tP{X=0,Y=1) =0.00013+0.19987 =0.20000, P{X=1}=P{X=1,Y=0}+P{X=1,Y=1} =0.00004+0.79996 =0.80000, P{Y=0}=P{X=0,Y=0}+P{X=1,Y=0} =0.00013+0.00004 三 0.00017, P{Y=1}=P{X=0,Y=1}+PX=1,Y=1} 0.19987+0.79996 =0.99983
解: 例2: (打开书P59) 求例3.2.2中 (X,Y) 的分量 X和Y的边缘分布。 P{X=0}= P{X=0, Y=0}+P{X=0, Y=1} = 0.00013+0.19987 = 0.20000, P{X=1}= P{X=1, Y=0}+P{X=1, Y=1} = 0.00004+0.79996 = 0.80000, P{Y=0}= P{X=0, Y=0}+P{X=1, Y=0} = 0.00013+0.00004 = 0.00017, P{Y=1}= P{X=0, Y=1}+P{X=1, Y=1} = 0.19987+0.79996 = 0.99983
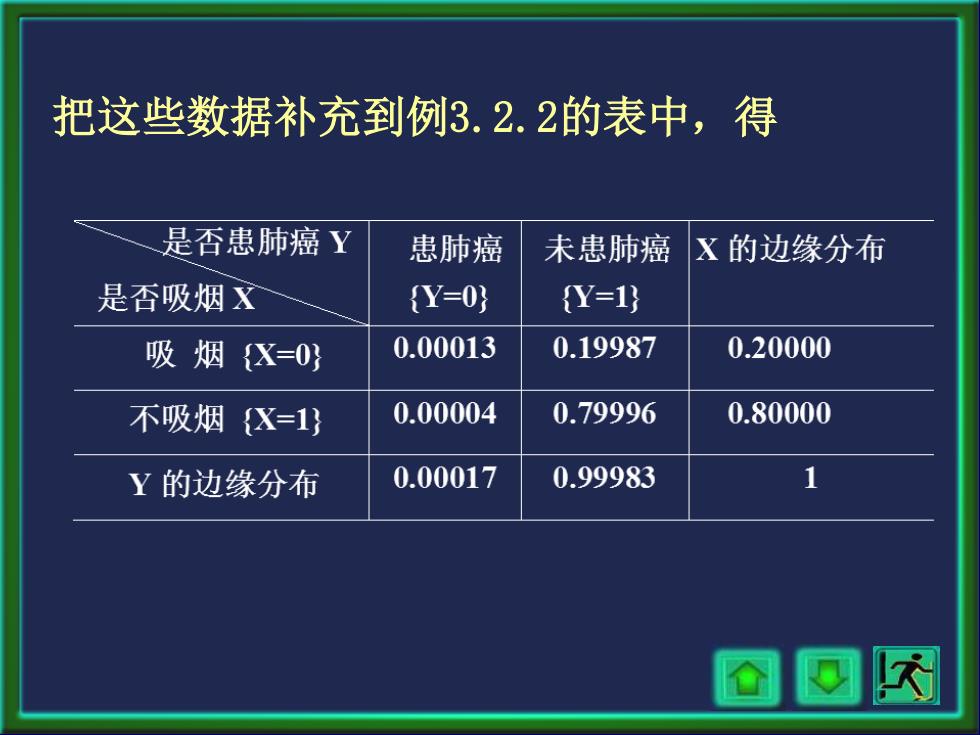
把这些数据补充到例3.2.2的表中,得 是否患肺癌Y 患肺癌 未患肺癌 X的边缘分布 是否吸烟X Y=0} Y=1} 吸烟{X=0} 0.00013 0.19987 0.20000 不吸烟X=1} 0.00004 0.79996 0.80000 Y的边缘分布 0.00017 0.99983 1 @@风网
把这些数据补充到例3.2.2的表中,得

3.4.2连续型随机向量的边缘概率密度 若化,)的联合概率密度为f化,y),则 X的边缘概率密度为 fx(x)=["f(x,y)dy, Y的边缘概率密度为 f(y)=[f(x,y)dx @@的
3.4.2 连续型随机向量的边缘概率密度 若 (X, Y) 的联合概率密度为 f (x, y),则 X的边缘概率密度为 Y 的边缘概率密度为 ( ) ( , ) , − f x = f x y dy X ( ) ( , ) . − f y = f x y dx Y

例3:若(X,)服从矩形区域a≤x≤b,c≤y≤d 上均匀分布,则边缘概率密度分别为 fy(y)=d-c y∈[c,d, fx(x)= b-a 0 xa,b]: y c,d]. 注:本例中X与都是服从均匀分布的随机变 量。但对其它非矩形区域上的均匀分布不一 定有上述结论。 四网
例3:若(X,Y)服从矩形区域 a≤x≤b,c≤y≤d 上均匀分布,则边缘概率密度分别为 − = 0, x [a,b]; , x [a,b], b a 1 f (x) X − = 0, y [c,d]. , y [c,d], d c 1 f (y) Y 注:本例中X与Y都是服从均匀分布的随机变 量。 但对其它非矩形区域上的均匀分布不一 定有上述结论

例4:设(X,)服从单位圆域x2+2≤1上的均 匀分布。求X和的边缘概率密度。 解: (x,)ED. (x,y)¥D 当x>1时, fx (x)=[f(x,y)dy=["Ody=0; @四函
例4:设(X,Y)服从单位圆域 x 2+y 2≤1上的均 匀分布。求X和Y的边缘概率密度。 = 0 ( , ) . ( , ) , 1 ( , ) x y D x y D f x y , , 解: 当|x|>1时, ( ) = ( , ) = 0 = 0; − − f x f x y d y d y X