
§2.3连续型随机变量 连续型随机变量X所有可能取值充满若 干个区间。对这种随机变量,不能象离散型 随机变量那样,指出其取各个值的概率,给 出概率分布。而是用“概率密度函数”表示 随机变量的概率分布
连续型随机变量X所有可能取值充满若 干个区间。对这种随机变量,不能象离散型 随机变量那样, 指出其取各个值的概率, 给 出概率分布。而是用“概率密度函数”表示 随机变量的概率分布。 §2.3 连续型随机变量

2.3.1频率直方图 例1:某工厂生产一种零件,由于生产过程中各 种随机因素的影响,零件长度不尽相同。现测 得该厂生产的100个零件长度(单位:mm)如下: 129,132,136,145,140,145,147,142,138,144,147,142,137,144,144, 134,149,142,137,137,155,128,143,144,148,139,143,142,135,142, 148,137,142,144,141,149,132,134,145,132,140,142,130,145,148, 143,148,135,136,152,141,146,138,131,138,136,144,142,142,137, 141,134,142,133,153,143,145,140,137,142,150,141,139,139,150, 139,137,139,140,143,149,136,142,134,146,145,130,136,140,134, 142,142,135,131,136,139,137,144,141,136. 这100个数据中,最小值是128,最大值是155
例1:某工厂生产一种零件,由于生产过程中各 种随机因素的影响,零件长度不尽相同。现测 得该厂生产的100个零件长度(单位: mm)如下: 2.3.1 频率直方图 129, 132, 136, 145, 140, 145, 147, 142, 138, 144, 147, 142, 137, 144, 144, 134, 149, 142, 137, 137, 155, 128, 143, 144, 148, 139, 143, 142, 135, 142, 148, 137, 142, 144, 141, 149, 132, 134, 145, 132, 140, 142, 130, 145, 148, 143, 148, 135, 136, 152, 141, 146, 138, 131, 138, 136, 144, 142, 142, 137, 141, 134, 142, 133, 153, 143, 145, 140, 137, 142, 150, 141, 139, 139, 150, 139, 137, 139, 140, 143, 149, 136, 142, 134, 146, 145, 130, 136, 140, 134, 142, 142, 135, 131, 136, 139, 137, 144, 141, 136. 这100个数据中,最小值是128,最大值是155。 155 128

作频率直方图的步骤 (1).先确定作图区间[a,们; a=最小数据-e/2,b=最大数据+ε/2, ε是数据的精度。 本例中8=1,a=127.5,b=155.5。 (2).确定数据分组数m=[1.87X(m-1)25+1] 组距d=(b-d/m, 子区间端点t=a+id,i=0,1,··,m
作频率直方图的步骤 (1). 先确定作图区间 [a, b] ; a = 最小数据-ε/ 2,b = 最大数据+ε/ 2, ε 是数据的精度。 本例中 ε = 1, a = 127.5, b = 155.5 。 (2). 确定数据分组数 m = [1.87×(n−1)2/5 + 1], 组距 d = (b − a) / m, 子区间端点t i = a + i d, i = 0, 1, · · · , m;
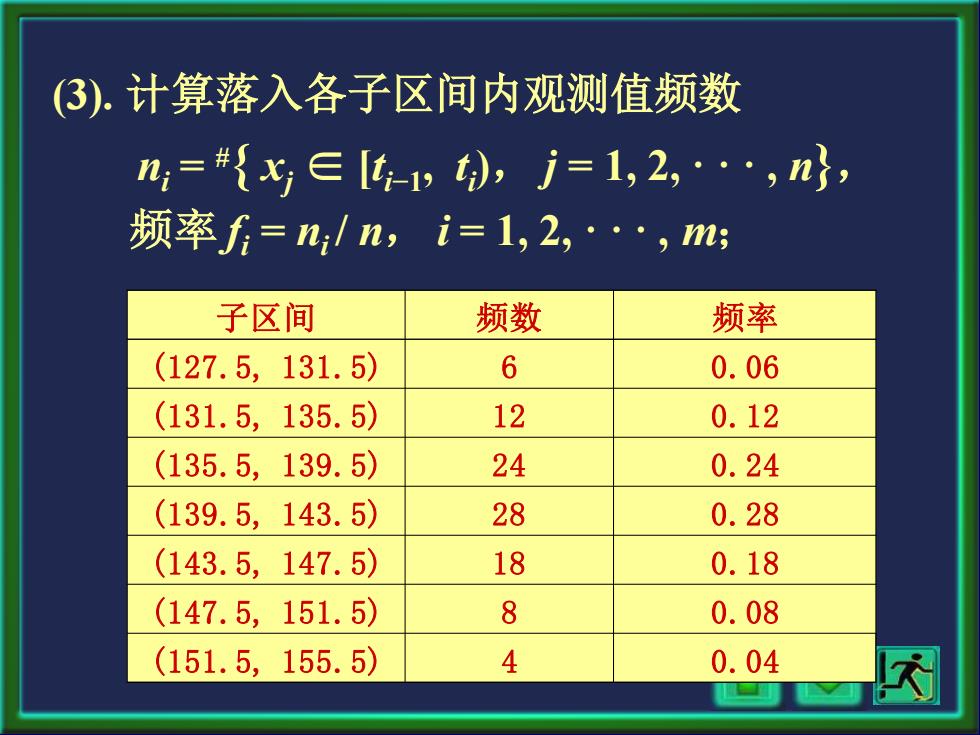
(3).计算落入各子区间内观测值频数 n=#{x,∈[t-1,t),j=1,2,··,n}, 频率f=n,/n,i=1,2,·,ms 子区间 频数 频率 (127.5,131.5) 6 0.06 (131.5,135.5) 12 0.12 (135.5,139.5) 24 0.24 (139.5,143.5) 28 0.28 (143.5,147.5) 18 0.18 (147.5,151.5) 8 0.08 (151.5,155.5) 4 0.04
(3). 计算落入各子区间内观测值频数 ni = #{ xj ∈ [t i−1, t i ), j = 1, 2, · · · , n}, 频率 fi = ni / n, i = 1, 2, · · · , m; 子区间 频数 频率 (127.5, 131.5) 6 0.06 (131.5, 135.5) 12 0.12 (135.5, 139.5) 24 0.24 (139.5, 143.5) 28 0.28 (143.5, 147.5) 18 0.18 (147.5, 151.5) 8 0.08 (151.5, 155.5) 4 0.04
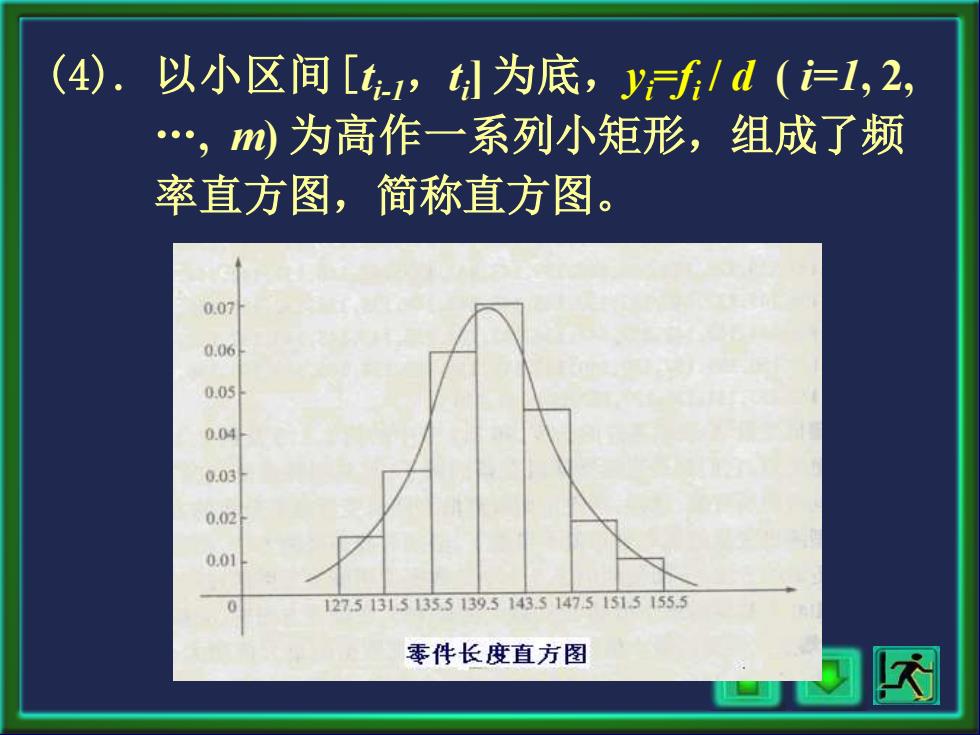
(4). 以小区间[,孙为底,yf1d(,2, .,m为高作一系列小矩形,组成了频 率直方图,简称直方图。 0.0 0.06 0.05 0.04 0.03 0.02 0.01 127513151355139.5143.5147.515151553 零件长度直方图 网
(4). 以小区间[t i-1,t i ] 为底,yi =fi / d ( i=1, 2, . , m) 为高作一系列小矩形,组成了频 率直方图,简称直方图