
两个探索性训练的案例 (顾P169) 例1如图,是一个边长为3的立方体,它 有27个小立方体,其中19个看得见,8个 看不见。问: ·(1)边长为4怎样? ■(2)边长为5呢? ■(3)任何大小呢? ■思路:数据分析,结构证明,直觉创造
两个探索性训练的案例(顾P169) ◼ 例1 如图,是一个边长为3的立方体,它 有27个小立方体,其中19个看得见,8个 看不见。问: ◼ (1)边长为4怎样? ◼ (2)边长为5呢? ◼ (3)任何大小呢? ◼ 思路:数据分析,结构证明,直觉创造
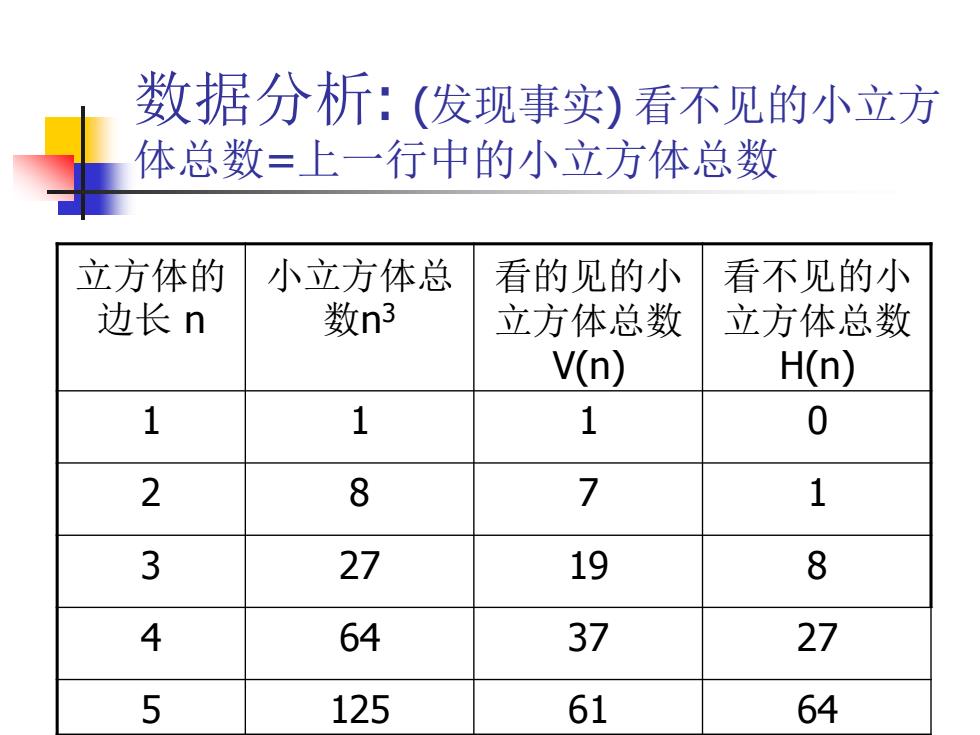
数据分析:(发现事实)看不见的小立方 体总数=上一行中的小立方体总数 立方体的 小立方体总 看的见的小 看不见的小 边长n 数n3 立方体总数 立方体总数 V(n) H(n) 1 1 1 0 2 8 7 1 3 27 19 8 4 64 37 27 5 125 61 64
数据分析: (发现事实) 看不见的小立方 体总数=上一行中的小立方体总数 立方体的 边长 n 小立方体总 数n 3 看的见的小 立方体总数 V(n) 看不见的小 立方体总数 H(n) 1 1 1 0 2 8 7 1 3 27 19 8 4 64 37 27 5 125 61 64

结构证明: 分顶面、前面、侧面三个面将看得见的 小立方体数目加起来 ■项面:n2;前面:n(n-1)=n2-n;侧面: (n-1)n-1)=n2-2n+1 ■所以V(n)=3n2-3n+1 计算看不见的小立方体总数:H(n)=n3-3 n2+3n-1=(n-1)3
结构证明: ◼ 分顶面、前面、侧面三个面将看得见的 小立方体数目加起来 ◼ 顶面:n 2;前面:n(n-1) =n2 -n;侧面: (n-1)(n-1)= n2 -2n+1 ◼ 所以V(n)=3 n2 -3n+1 ◼ 计算看不见的小立方体总数:H(n)= n3 -3 n 2 +3n-1= (n-1)3

直觉创造: 剥去看得见的顶面、前面、侧面三个面,剩下 的就是上一行的立方体 这个例子给出三种不同的问题解决思路,隐含 的对学生知识和能力上的要求: ·几何和测量概念(三维图形,递增序列) ■函数和代数概念(公式、表格、猜想、表达式) ■数学技能和相关工作(制作运用粗略表格和图式, 提高理解力) ·数学交流(学生自行筹划,表示数学步骤和结果)
直觉创造: ◼ 剥去看得见的顶面、前面、侧面三个面,剩下 的就是上一行的立方体 ◼ 这个例子给出三种不同的问题解决思路,隐含 的对学生知识和能力上的要求: ◼ 几何和测量概念(三维图形,递增序列) ◼ 函数和代数概念(公式、表格、猜想、表达式) ◼ 数学技能和相关工作(制作运用粗略表格和图式, 提高理解力) ◼ 数学交流(学生自行筹划,表示数学步骤和结果)

例2传染病传播的数学模型 己知传染病传播的数学模型为Hk+1=Hk -aHk +BSkHk,其中,Hk+1表示第k+1天的患病人数, Hk表示第k天的患病人数,表示每天的痊愈率, B表示每天的发病率;oHk为第k天的痊愈人数, BSKHK为第k天新发病人数,这里的Sk是考虑免 疫原因计算第k天可能感染人数时的系数。 ,(1)利用递推关系式预测若干天后的患病人 数,以便于医疗疾控部门决策; (2)计算增量AHk=Hk+1Hk=(BSk)Hk,BSk =0是临界点,临界值C:Sk=0/β
例2 传染病传播的数学模型 ◼ 已知传染病传播的数学模型为Hk+1 =Hk -Hk +SkHk ,其中, Hk+1表示第k+1天的患病人数, Hk表示第k天的患病人数, 表示每天的痊愈率, 表示每天的发病率; Hk为第k天的痊愈人数, SkHk为第k天新发病人数,这里的Sk是考虑免 疫原因计算第k天可能感染人数时的系数。 ◼ (1)利用递推关系式预测若干天后的患病人 数,以便于医疗疾控部门决策; ◼ (2)计算增量Hk=Hk+1 -Hk =(Sk -)Hk , Sk - =0是临界点,临界值C:Sk=/