
第一节多元函数的基本概念平面点集多元函数概念三、多元函数的极限四、多元函数的连续性返回MathGS公式上页下页线与面数学家
第一节 多元函数的基本概念 一、平面点集 二、多元函数概念 三、多元函数的极限 四、多元函数的连续性

第一节多元函数的基本概念一、平面点集1.邻域设Po(xo,Jo)是xOy平面上的一个点,是某一正数,与点Po(xo,yo)距离小于S的点P(x,J)的全体,称为点Po的S邻域,记作U(P。,),即U(P,)=(PIIPP<S) :也就是U(P,) =((x, y)/ /(x-xo)? +(y-yo)? <S)返回MathGS公式数学家上页下页线与面
第一节 多元函数的基本概念 一、平面点集 1. 邻域 设P0 (x0 , y0 )是xOy平面上的一个点,是某一正数, 与点P0 (x0 , y0 )距离小于 的点P(x , y)的全体,称为点P0 的 邻域,记作 U(P0 , ),即 ( , ) { | | | }, U P0 = P PP0 也就是 ( , ) {( , )| ( ) ( ) }. 2 0 2 U P0 = x y x − x0 + y − y
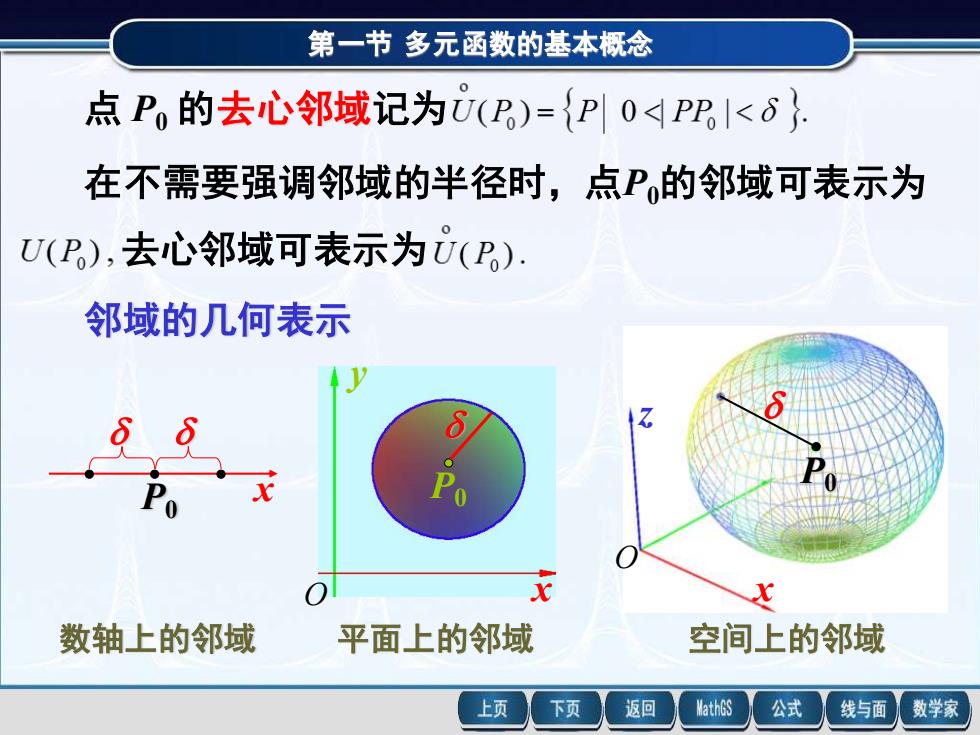
第一节多元函数的基本概念点P。的去心邻域记为(P)={P0PP<在不需要强调邻域的半径时,点P.的邻域可表示为U(P),去心邻域可表示为U(P)邻域的几何表示SZ8d9PPo十POx0x空间上的邻域数轴上的邻域平面上的邻域MathGS上页下页返回公式线与面数学家
第一节 多元函数的基本概念 点 P0 的去心邻域记为 在不需要强调邻域的半径时,点P0的邻域可表示为 去心邻域可表示为 邻域的几何表示 P0 O x y 平面上的邻域 x 数轴上的邻域 P0 P0 x z 空间上的邻域 O
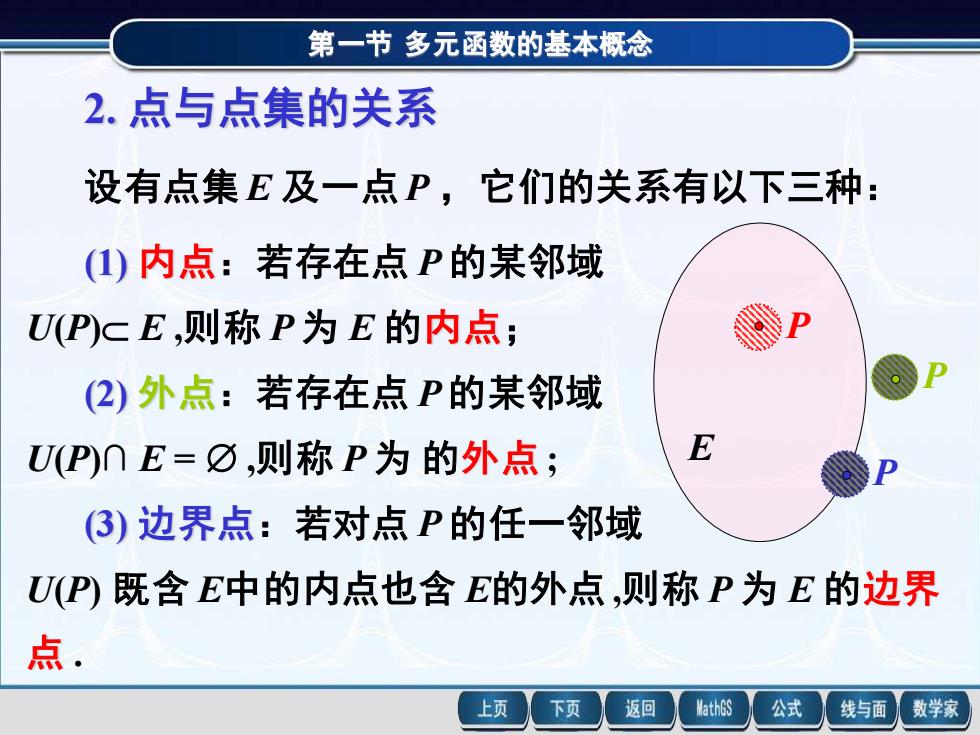
第一节多元函数的基本概念2.点与点集的关系设有点集E及一点P,它们的关系有以下三种(1)内点:若存在点P的某邻域U(P)CE,则称P为E的内点(2)外点:若存在点P的某邻域EU(P)N E=の ,则称 P为 的外点P(3)边界点:若对点P的任一邻域U(P既含E中的内点也含E的外点,则称P为E的边界点下页返回MathGS公式上页线与面数学家
第一节 多元函数的基本概念 E 2. 点与点集的关系 设有点集 E 及一点 P ,它们的关系有以下三种: (1) 内点:若存在点 P 的某邻域 (2) 外点:若存在点 P 的某邻域 (3) 边界点:若对点 P 的任一邻域 U(P) E ,则称 P 为 E 的内点; U(P)∩ E = ,则称 P 为 的外点 ; U(P) 既含 E中的内点也含 E的外点 ,则称 P 为 E 的边界 点 . P P P

第一节多元函数的基本概念E的边界点的全体,称为E的边界,记作aE,由定义可知,E的内点一定属于E,E的外点一定不属于E,E的边界点可能属于E,也可能不属于E聚点:如果对于任意给定的正数8,点P的去心邻域ü(P。,S)内总有E中的点,则称P是E的聚点聚点可以属于E,也可以不属于E(因为聚点可以为E的边界点)MathGS上页下页返回公式线与面数学家
第一节 多元函数的基本概念 E的边界点的全体,称为E的边界,记作 E . 由定义可知,E的内点一定属于E,E的外点一定不 属于E,E的边界点可能属于E,也可能不属于E. 聚点: 如果对于任意给定的正数 ,点 P 的去心邻 域 内总有E中的点,则称P是E的聚点. 聚点可以属于 E , 也可以不属于E (因为聚点可以为 E 的边界点).