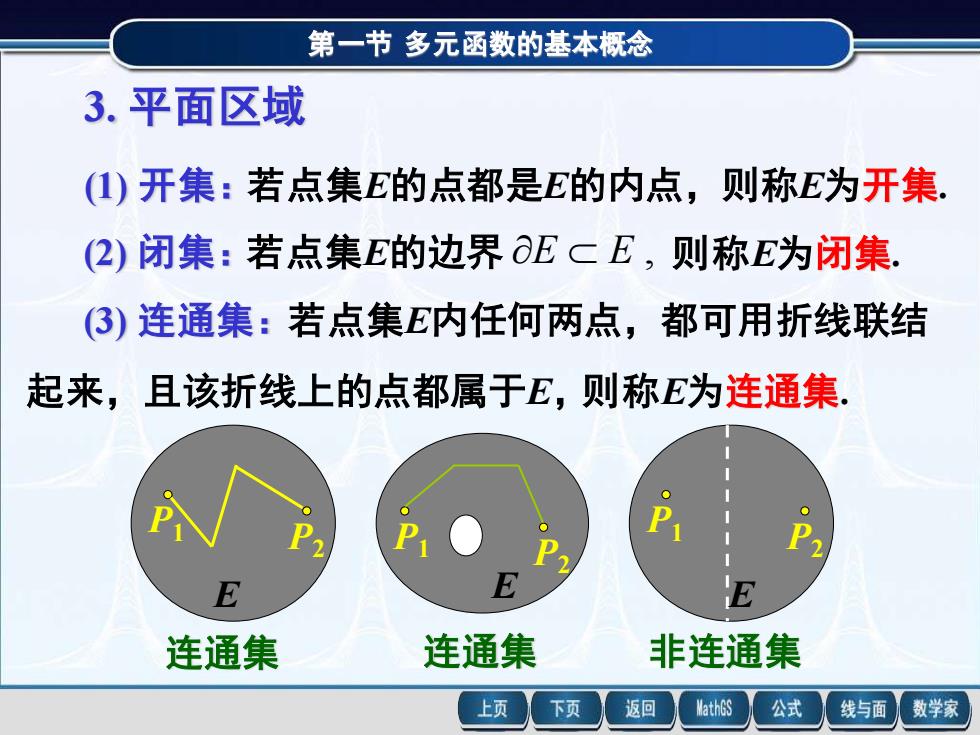
第一节多元函数的基本概念3.平面区域(1)开集:若点集E的点都是E的内点,则称E为开集(2)闭集:若点集E的边界aECE,则称E为闭集(3)连通集:若点集E内任何两点,都可用折线联结起来,且该折线上的点都属于E,则称E为连通集.PPBP2PPEEE连通集非连通集连通集返回MathGS公式上页下页线与面数学家
第一节 多元函数的基本概念 3. 平面区域 (1) 开集:若点集E的点都是E的内点,则称E为开集. (2) 闭集:若点集E的边界 E E , 则称E为闭集. (3) 连通集:若点集E内任何两点,都可用折线联结 起来,且该折线上的点都属于E,则称E为连通集. E P1 P2 E P1 P2 E P1 P2 连通集 连通集 非连通集

第一节多元函数的基本概念(4)区域(或开区域):连通的开集称为区域或开区域(5)闭区域:开区域同它的边界一起所构成的点集称为闭区域(6)有界集:对于平面点集E,如果存在某一正数r,使得EcU(O,r)其中O是坐标原点,则称E为有界集(7)无界集:一个集合如果不是有界集,就称这集合为无界集返回MathGS公式数学家上页下页线与面
第一节 多元函数的基本概念 (4) 区域(或开区域):连通的开集称为区域或开区域. (5) 闭区域:开区域同它的边界一起所构成的点集称 为闭区域. (6) 有界集:对于平面点集E,如果存在某一正数 r, 使得 E U(O , r) , 其中O是坐标原点,则称E为有界集. (7) 无界集:一个集合如果不是有界集,就称这集合 为无界集.

第一节多元函数的基本概念例如,集合 ((x,)[1<x2+2<2),是区域、有界集集合 ((x,)[1≤x2+2≤2),是闭区域、有界集集合(x,)[1<x2+2≤2),既非开集,也非闭集XxX有界开区域有界闭区域非开非闭,但有界MathGS上页下页返回公式线与面数学家
第一节 多元函数的基本概念 例如, 集合 {( , )|1 2}, 2 2 x y x + y 是区域、有界集. 集合 {( , )|1 2}, 2 2 x y x + y 是闭区域、有界集. 集合 {( , )|1 2}, 2 2 x y x + y 既非开集,也非闭集. 有界开区域 x y O 有界闭区域 x y O 非开非闭,但有界 x y O

第一节多元函数的基本概念*4.n维空间n元有序数组(x,x2,,x)的全体所构成的集合记作Rn,即J Rn=RxRx...xR={(xi,x2,..,xn)| x R, k=1,2,...,n ).Rn中的每一个元素用单个粗体字母x表示,即x=(x,x2,,xn).任给 x=(xi,X2,...,xn), y=(y1,y2,..,yn)eR" , aeR,定义:x+y=(xi+yi,X2+y2,",xn+yn),线性运算ax=(ax, ax2, ..., axn).MathGS下页返回公式线与面数学家上页
第一节 多元函数的基本概念 *4. n 维空间 n 元有序数组 的全体所构成的集合记作 Rn , 即 R = R R R n Rn中的每一个元素用单个粗体字母 x 表示, 即 定义: ( , , , ) . 1 2 n x = x x x ( , , , ) , 1 1 2 2 n n x + y = x + y x + y x + y 线性运算 任给

第一节多元函数的基本概念其元素称为点定义了线性运算的R称为n维空间或n维向量.x;称为x的第i个坐标或第i个分量特别地,Rn中的零元0称为Rn中的坐标原点或n维零向量.Rn中的两点x=(xi,,xn),=(yi,,yn)的距离定义为p(x, y)=x-yl= /(xi -y) +..+(x, -yn)?这种距离称为欧氏距离返回MathGS公式上页下页线与面数学家
第一节 多元函数的基本概念 其元素称为点 或n 维向量. xi 称为 x 的第 i 个坐标或第 i 个分量. 定义了线性运算的Rn称为 n 维空间, 特别地,Rn中的零元0称为Rn中的坐标原点或n维零 向量. 定义为 ( , , ) , ( , , ) 1 n 1 n R x = x x y = y y n中的两点 的距离 这种距离称为欧氏距离.