
第十章第四节重积分的应用一、立体体积曲面的面积三、物体的质心四、物体的转动惯量五、物体的引力HIGH EDUCATION PRESS返回结束机动自录上页下页
第四节 一、立体体积 二、曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力 机动 目录 上页 下页 返回 结束 重积分的应用 第十章

一、立体体积·曲顶柱体的顶为连续曲面 z=f(x,y),(x,y)ED则其体积为V = JJ f(x, y)doD·占有空间有界域Q的立体的体积为dxdydz一HIGH EDUCATION PRESS机动上页下页返回结束自录
一、立体体积 • 曲顶柱体的顶为连续曲面 则其体积为 • 占有空间有界域 的立体的体积为 机动 目录 上页 下页 返回 结束
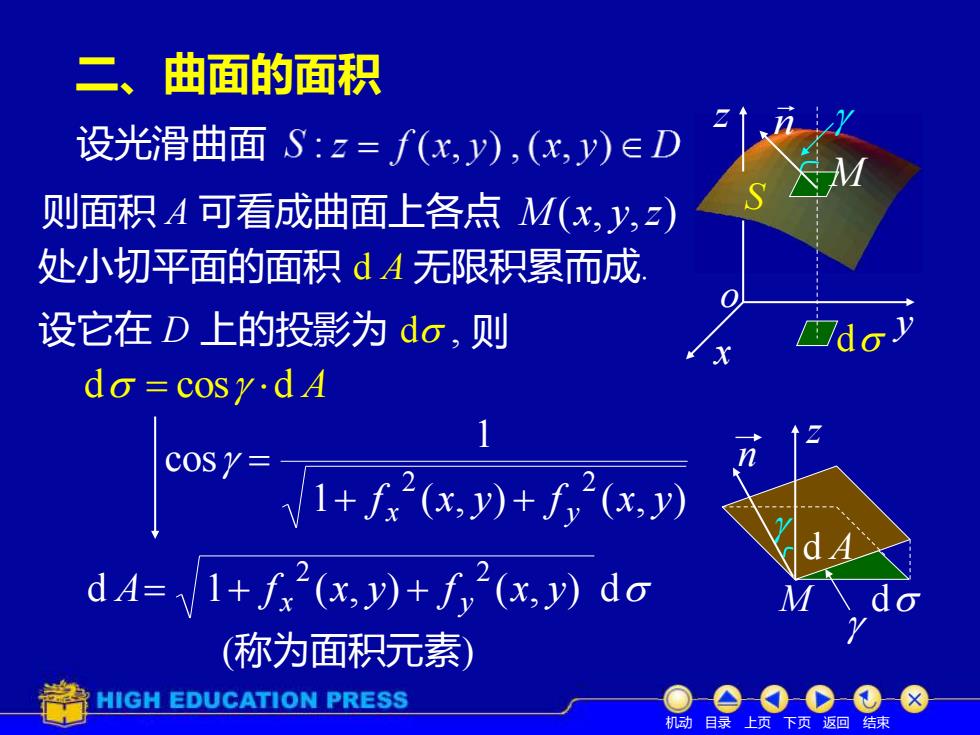
二、曲面的面积设光滑曲面S:z= f(x,y),(x,y)eDSMS则面积A可看成曲面上各点 M(x,y,z)处小切平面的面积dA无限积累而成设它在D 上的投影为 do,则dado =cosy.d AnCOSY=1+ fx(x,y)+ f,(x,y)C/1+ fx(x,y)+f,'(x,y) dodA=1Mdo(称为面积元素)HIGH EDUCATION PRESS上页下页返回结束机动目录
M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A 可看成曲面上各点 M (x, y,z) 处小切平面的面积 d A 无限积累而成. 设它在 D 上的投影为 d , d = cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y (称为面积元素) 则 M n d 机动 目录 上页 下页 返回 结束

故有曲面面积公式A= f /1+f(x,y)+ f,'(x,y) do即dxdyHIGH EDUCATION PRESS机动目录上页返回结束下页
故有曲面面积公式 即 机动 目录 上页 下页 返回 结束
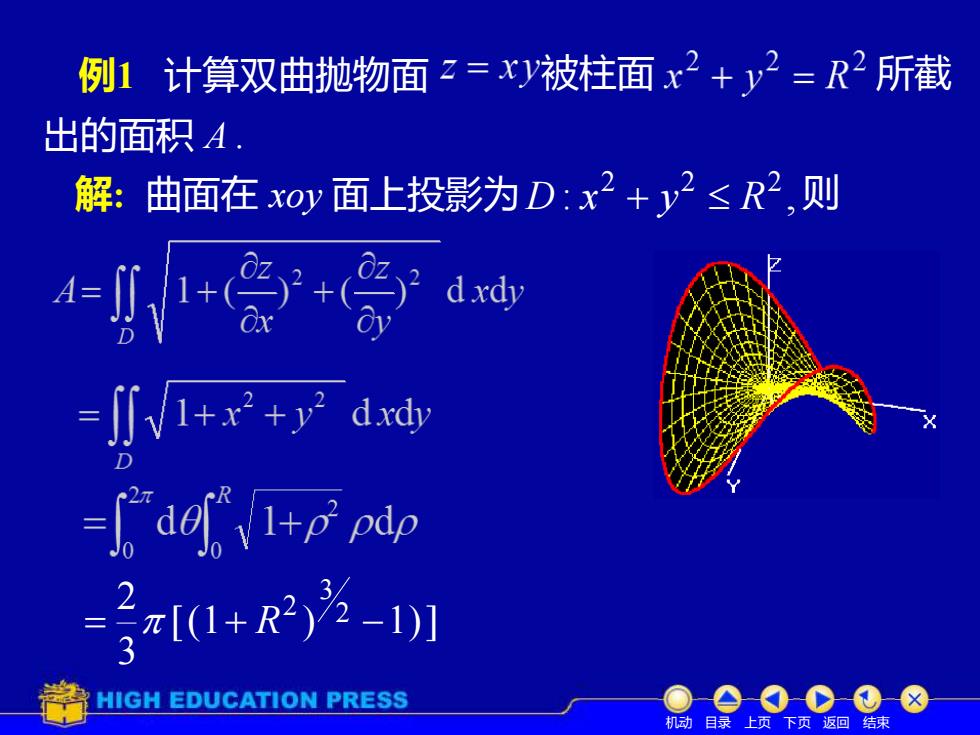
例1计算双曲抛物面z=xy被柱面2+2=R2所截出的面积 A解:曲面在 xoy面上投影为D:x2+2≤R2,则dxdy福1+x? +y?dxdyRde1+ppdp元[(1+ R2) -1)]HIGH EDUCATION PRESS上页下页返回结束机动自录
例1 计算双曲抛物面 被柱面 所截 解: 曲面在 xoy 面上投影为 : , 2 2 2 D x + y R 则 [(1 ) 1)] 3 2 2 3 2 = + R − 出的面积 A . 机动 目录 上页 下页 返回 结束