
第节 函数的连续性与间断点函数的连续性二、 函数的间断点三、小结 思考题
第八节 函数的连续性与间断点 • 一、函数的连续性 • 二、函数的间断点 • 三、小结 思考题

函数的连续性1.函数的增量设变量u从它的一个初值u变到终值u,,终值与初值的差u,一u就叫做变量u的增量,记作Au即Au = u, -ur.注意:△u可以是正数也可以是负数
一、函数的连续性 1.函数的增量 1 2 2 1 2 1 . u u u u u u u u u u 设变量 从它的一个初值 变到终值 ,终值与 初值的差 就叫做变量 的增量,记作 , 即 注意:u可以是正数也可以是负数
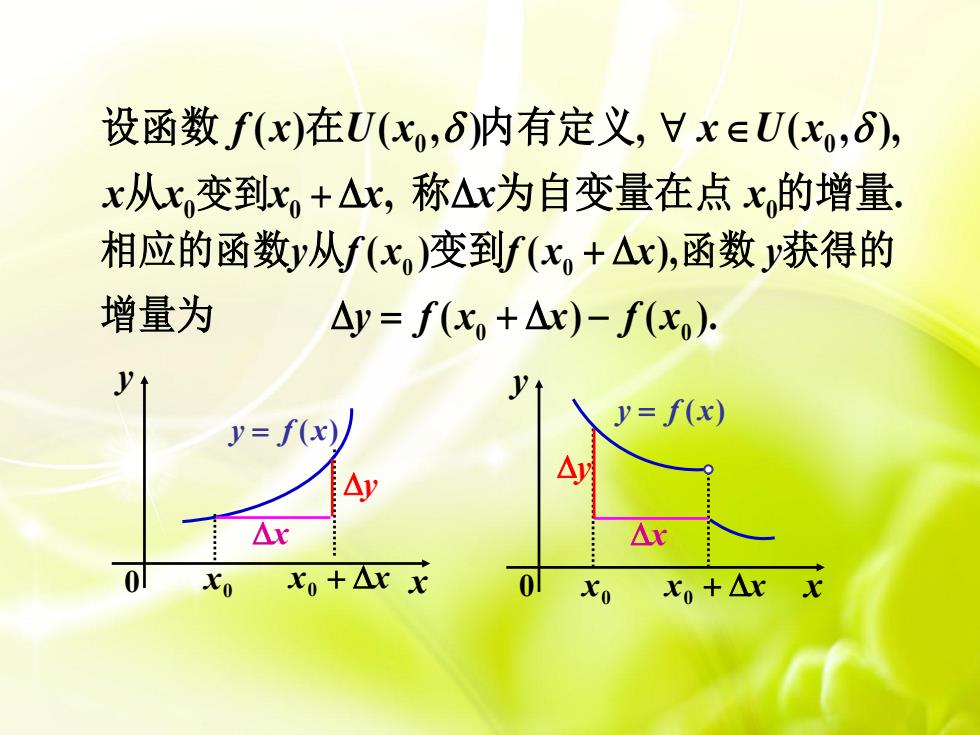
设函数 f(x)在U(xo,S)内有定义,V xeU(xo,),x从x变到x+△x,称Ax为自变量在点x,的增量相应的函数y从f(x,)变到f(x,+Ax),函数y获得的增量为Ay= f(x, +△r)- f(x)yyty=f(x)y=f(x))AyAyAxAr01xo+Ax xxo01xXo+AxXo
0 0 0 0 0 ( ) ( , ) , ( , ), , . f x U x x U x x x x x x x 变到 设函数 在 内有定义 从 称 为自变量在点 的增量 0 0 0 0 ( ) ( ), ( ) ( ). y f x f x x y y f x x f x 相应的函数 从 变到 函数 获得的 增量为 x y 0 0 x x x 0 y f ( x) x y x y 0 0 x x x 0 x y y f ( x)

2.连续的定义定义设函数y= f(x)在点x,的某个邻域内有定义,如果lim Ay = lim[f(x, + △x)- f(x,)] = 0Ax>0Ar-→0那么就称函数y=f(x)在点x,处连续设 x= x + △x,Ay= f(x)- f(x,),Ax→0 就是x→x,Ay→0就是 f(x)→f(x,)
2.连续的定义 , 0 设 x x x ( ) ( ), 0 y f x f x 0 x x x 0 , 就是 0 ( ) ( ). 0 y 就是 f x f x 0 0 0 0 0 0 ( ) lim lim[ ( ) ( )] 0 ( ) . x x y f x x y f x x f x y f x x 设函数 在点 的某个邻域内有定义, 如果 那么就 定 称函数 在点 处连续 义

定义设函数y= f(x)在点x,的某个邻域内有定义,如果lim f(x) = f(x)x-→xo那么就称函数y=f(x)在点x,处连续"-S"定义:>0,>0,使当x-x<时,恒有|f(x)-f(x,)<8
"": 定义 0 0 0, 0, , ( ) ( ) . x x f x f x 使当 时 恒有 0 0 0 0 ( ) lim ( ) ( . ) ( ) x x y f x x f x f x y f x x 设函数 在点 的某个邻域内有定义, 如果 那么就 定义 称函数 在点 处连续