
第二节定积分在几何上的应用、平面图形的面积二、体积三、平面曲线的弧长
第二节 定积分在几何上的应用 一、平面图形的面积 二、体 积 三、平面曲线的弧长

第六章定积分的应用一、平面图形的面积1.直角坐标情形AyAy=f2(x)y=f(x)y=f(x)Xxooxx+Axbb9axAx曲边梯形的面积曲边梯形的面积brbA=f(x)dxA =[f2(x) - fi(x)]dxaa第二节定积分在几何上的应用
第二节 定积分在几何上的应用 第六章 定积分的应用 一、平面图形的面积 1. 直角坐标情形 曲边梯形的面积 曲边梯形的面积
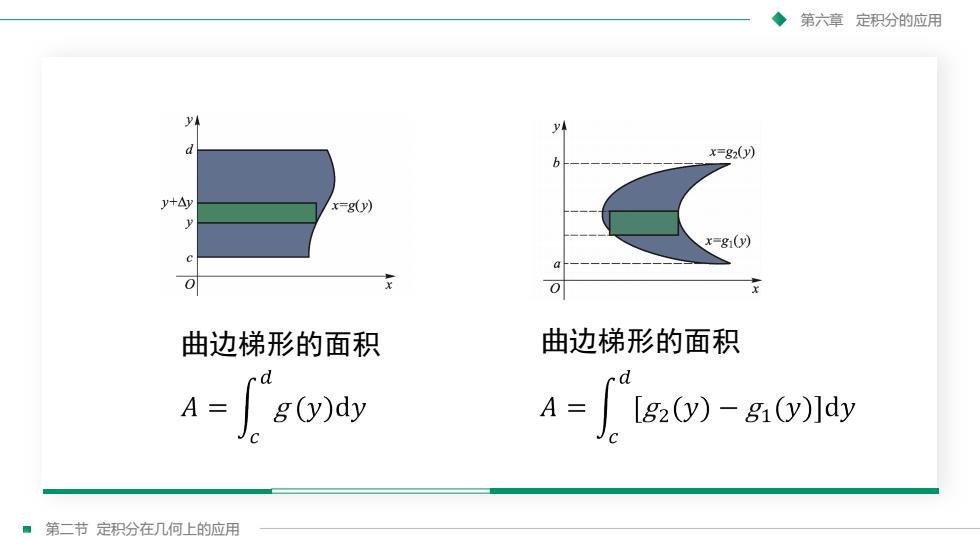
第六章定积分的应用yAVIdx=g2(y)y+Ayx=g(y)x=g1()caxo0x曲边梯形的面积曲边梯形的面积.ddA =A =g (y)dy[g2(y) - gi(y)]dy第二节定积分在几何上的应用
第二节 定积分在几何上的应用 第六章 定积分的应用 曲边梯形的面积 曲边梯形的面积
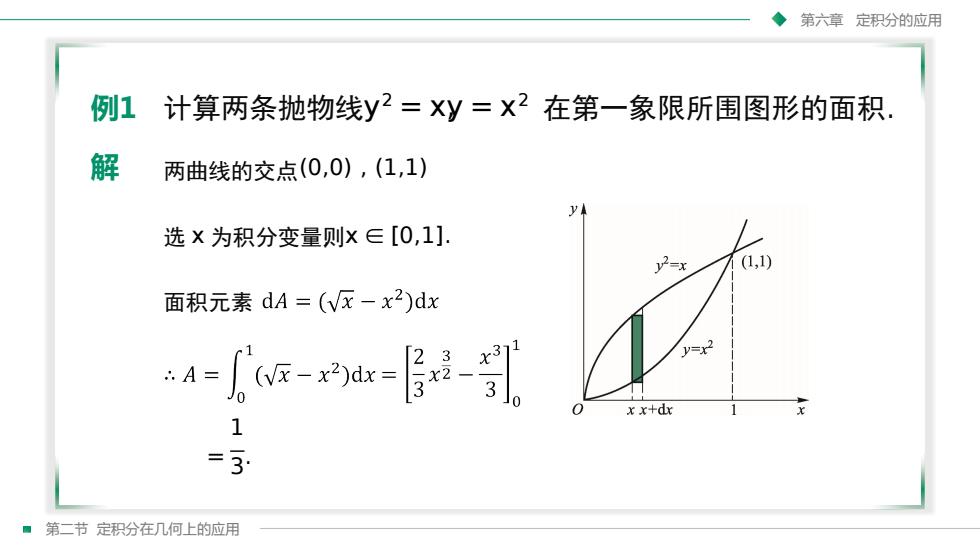
第六章定积分的应用计算两条抛物线y2=xy=x2在第一象限所围图形的面积例1解两曲线的交点(0,0),(1,1)y选×为积分变量则xE[0,1].(1,1)s面积元素dA=(Vx一x2)dx1332:A=(vx -dx:x23Jox0xx+dx1= 3.第二节定积分在几何上的应用
第二节 定积分在几何上的应用 第六章 定积分的应用 = 1 3 . 面积元素 选 x 为积分变量,则x ∈ [0,1]. 两曲线的交点(0,0) , (1,1) 计算两条抛物线y 2 = x,y = x 2 在第一象限所围图形的面积. 解 例1

第六章定积分的应用例2计算抛物线y2=2x与直线y=×-4所围图形的面积解两曲线的交点(2,-2),(8,4)选取y作积分变量,-21则yE[-2,4](8, 4)y+dyydA = (y + 4 -面积元素di0x(2)(2,X1:A=(y+4-2= 18.4y223-2第二节定积分在几何上的应用
第二节 定积分在几何上的应用 第六章 定积分的应用 = 18. 面积元素 则y ∈ [ − 2,4] 选取y作积分变量, 两曲线的交点(2, − 2) , (8,4) 计算抛物线y 2 = 2x与直线y = x − 4所围图形的面积. 解 例2