
第二节微积分基本公式一、问题的提出二、积分上限的函数及其导数三、牛顿-莱布尼兹公式
第二节 微积分基本公式 一、问题的提出 二、积分上限的函数及其导数

第五章定积分一、问题的提出寻求一个计算定积分的有效简便的方法,段兼鞠炸直线运动,已知速度V=v(t)是时间间隔[T,T2]引例上t的一个连续函数,且v(t)≥0.求在运动时间内物体所解设s = s(t)是位置函数,则 s = s(T,)-s(T,),T0s(T))s(T2)s(t)v(t)dt又由定积分的定义可知S=:v(t)dt = s(T2)-s(Ti), s(t) =v(t)第二节积分上限的函数及其导数
第二节 积分上限的函数及其导数 第五章 定积分 一、问题的提出 解 引例 则 s = s(T2) − s(T1). 寻求一个计算定积分的有效简便的方法. 设某物体作直线运动, 已知速度v = v(t)是时间间隔[T1,T2] 上t的一个连续函数, 且v(t) ≥ 0. 求在运动时间内物体所 经过路程s. 设s = s(t)是位置函数, 又由定积分的定义可知 s ′ (t) = v(t)

第五章定积分二、积分上限函数及其导数1.积分上限函数的定义设函数f(x)在区间[ab]上连续,并且设x为[ab]上的一点,xf(t)dt记为 Φ(x)考察定积分f(x)dx =积分上限函数JaJaJ4如果上限x在区间[ab]上任意变动y=f(x)则对于每一个取定的X值,定积分有(E)@ (x)一个对应值,所以它在[ab]上定义了一个函数,X0Ex+Axbg这个函数的几何意义是如图阴影部分的面积函数第二节积分上限的函数及其导数
第二节 积分上限的函数及其导数 第五章 定积分 二、积分上限函数及其导数 考察定积分 1. 积分上限函数的定义 记为 积分上限函数 设函数f(x)在区间[a,b]上连续, 并且设x为[a,b]上的一点, 如果上限x在区间[a,b]上任意变动, 则对于每一个取定的x值, 定积分有 一个对应值,所以它在[a,b]上定义了 一个函数. Φ(x) 这个函数的几何意义是如图阴影部分的面积函数

第五章定积分2.积分上限函数的性质定理1如果f(x)在[ab]上连续,则积分上限的函数f(t)dtΦ(x) a在[ab]上可导,并且它的导数rxdf(t)dt =f(x)(a<x≤b)D!XdxJa即(x)是f(x)在[a,b]上的一个原函数第二节积分上限的函数及其导数
第二节 积分上限的函数及其导数 第五章 定积分 2. 积分上限函数的性质 (a ≤ x ≤ b) 定理1 如果f(x)在[a,b]上连续, 则积分上限的函数 在[a,b]上可导, 并且它的导数 即ᵯ(x)是f(x)在[a, b]上的一个原函数. 第二节 积分上限的函数及其导数 第五章 定积分
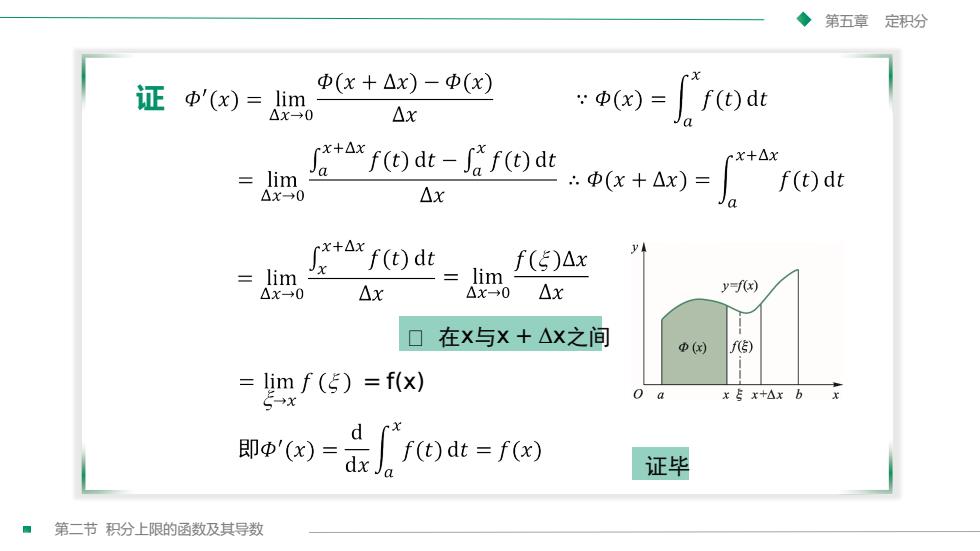
第五章定积分Φ(x + △x) -Φ(x)证Φ'(x)= lim: Φ(x) =f(t)dtAx4x→0fx+$* f(t) dt - J* f(t) dtx+AxPlim: Φ(x + Ax) =f(t)dt二AxAx→02rx+△xyAf(t) dtf()Ax3limlim-y=f(x)Axx4x-0Ax-0在x与x+△x之间f(E)@(x)= lim f () = f(x)oax=x+AxbxE-xcd即β'(x)f(t)dt = f(x)dxJa证毕第二节积分上限的函数及其导数
第二节 积分上限的函数及其导数 第五章 定积分 证 ᵯ 在x与x + Δx之间 = f(x) 证毕