
第十节闲区间上连续函数的性质有界性与最大值最小值定理二、零点定理与介质定理三、小结
第十节 闭区间上连续函数的性质 • 一、有界性与最大值最小值定理 • 二、零点定理与介质定理 • 三、小结

一、有界性与最大值最小值定理定义:对于在区间I上有定义的函数f(x),如果有xEI,使得对于任一xeI都有f(x)≤ f(x)(f(x)≥ f(x)则称f(x)是函数f(x)在区间I上的最大(小)值例如, y=1+ sin x,在[0,2元]上,Jmax =2,ymin =0;y = sgn x,在(-00,+o0)上, ymax = 1, ymin = -1;在(0, +o)上, Jmax = Ymin = 1
一、有界性与最大值最小值定理 0 0 0 0 ( ), , ( ) ( ) ( ( ) ( )) ( ) ( ) ( ) . I f x x I x I f x f x f x f x f x f x I 对于在区间 上有定义的函数 如果有 使得对于任一 都有 则称 是函数 在区间 上的最大 义 小 : 值 定 例如, max min y x y y sgn , ( , ) , 1, 1; 在 上 max min 在(0, ) , 1. 上 y ymax min y x y y 1 sin , [0,2 ] , 2, 0; 在 上
)在闭区间上连续定理1(最大值和最小值定理)的函数有界且一定能取得它的最大值和最小值Xy=f(x)y=f(x)X元0d42>注1.若区间是开区间,定理不一定成立;2.若区间内有间断点,定理不一定成立
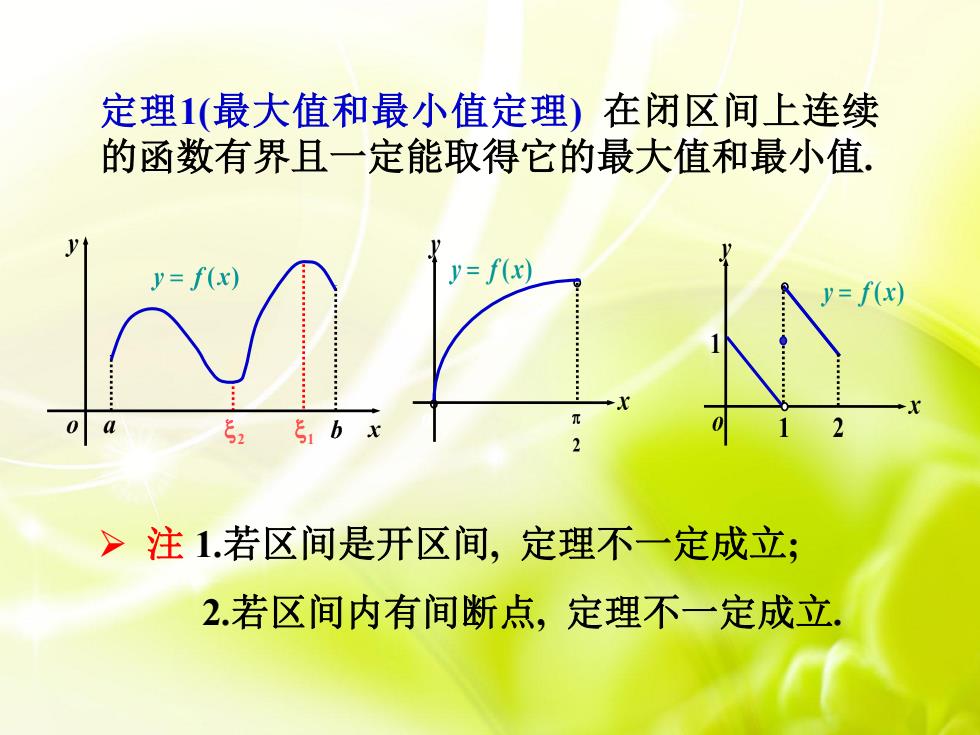
定理1(最大值和最小值定理) 在闭区间上连续 的函数有界且一定能取得它的最大值和最小值. 2 1 注 1.若区间是开区间, 定理不一定成立; 2.若区间内有间断点, 定理不一定成立. o

二、零点定理与介值定理定义:如果x,使f(x)=0,则x,称为函数f(x)的零点定理2(零点定理)设函数f(x)在闭区间[a,bl上连续且f(a)与f(b)异号(即f(a)·f(b)<0),那么在开区间(a,b)内至少有函数f(x)的一个零点,即至少有一点(a<<b), 使得f()= 0.即方程f(x)=0在(a,b)内至少存在一个实根
0 0 0 ( ) 0, ( ) . 定义 如果 x f x x f x 使 则 称为函数 的零点 : 二、零点定理与介值定理 即方程 f x a b ( ) 0 ( , ) . 在 内至少存在一个实根 ( ) [ , ] ( ) ( ) ( ( ) ( ) 0 2( ) ( , ) ( ) ( ) ) 0. ) ( f x a b f a f b f a f b a b f x a b f 设函数 在闭区间 上连续, 且 与 异号 即 ,那么在开区 间 内至少有函数 的一个零点,即至少有 一点 ,使得 定理 零点定理

几何解释:连续曲线弧y= f(x)的两个端点位于x轴的不同侧,则曲线弧与x轴至少有一个交点Vy=f(x)0aiEE3A6
3 2 1 几何解释: ( ) , . y f x x x 连续曲线弧 的两个端点位于 轴的 不同侧 则曲线弧与 轴至少有一个交点