>注(1)函数极限与f(x)在点x,是否有定义无关(2)x→x,的过程必须是双侧的(2).几何解释:yy= f(x)当x在x的去心邻A+EENEEEER域时,函数y= f(x)A图形完全落在以直A-β..ER线y=A为中心线,Sxo+sX-8xo0宽为2的带形区域内x显然,找到一个S后,8越小越好
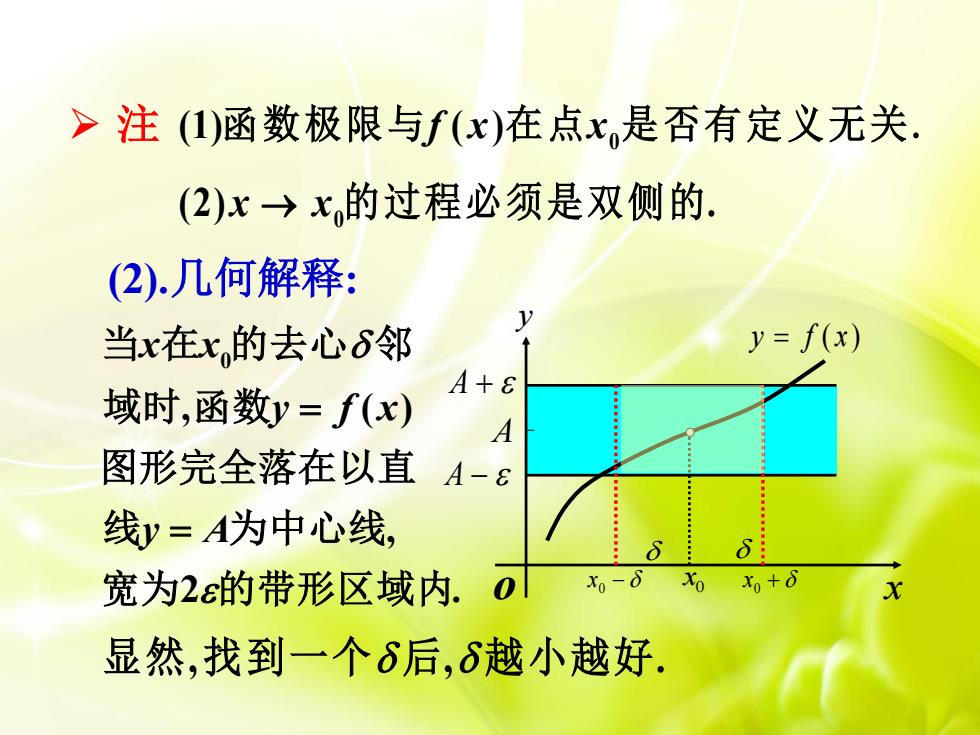
(2).几何解释: 0 , ( ) , 2 . x x y f x y A 当 在 的去心 邻 域时 函数 图形完全落在以直 线 为中心线 宽为 的带形区域内 0 (1) ( ) 函数极限与f x x 在点 是否有定义无关. 显然, , . 找到一个 后 越小越好 注 0 (2) . x x 的过程必须是双侧的 y f ( x ) A A A 0 x 0 x 0 x x y o

例1 证明 lim C = C,(C为常数)x→xo证任给ε>0,任取>0,当0<x-x<时,f(x)-A =C -Cl =0 <ε成立, :. lim C =C.x→xo例2 证明 lim x = xo.x→xo取8=8,证 :f(x)-A=x-xl,任给ε>0,当0<x-x|<8=8时,.:. lim x=Xo.f(x)-A=x-x<ε成立,x-→Xo
例 1 lim , ( ). 0 证 明 C C C为常数 x x 证 f ( x ) A C C 成立, 任给 0, 0 lim . 0 C C x x 任取 0, 0 , 当 x x0 时 例 2 lim . 0 0 x x x x 证 明 证 0 f x A x x ( ) , 任给 0, 取 , 0 , 当 x x0 时0 f ( x) A x x 成立, lim . 0 0 x x x x

r-1例3证明lim=2x→1 x-1证函数在点x=1处没有定义x2-1: f(x)- A=-2=|x -1任给>0,x-1只要取8= 8,要使|f(x)-A<8,2x当0<x-x<8时,就有2<8,x-1r:2.limx-1x-1
例3 2. 1 1 lim 2 1 x x x 证明 证 2 1 ( ) 2 1 x f x A x 任给 0, 只要取 , 0 , 当 x x0 时 函数在点x=1处没有定义. x 1 要 使 f ( x) A , 2 , 1 1 2 x x 就有 2. 1 1 lim 2 1 x x x

例4 证明:当x>0时,lim √x=x。x-→xox-xo证: |f(x)-A|=/x-/x|=x+/xo<x-xoVxoV>0,要使[f(x)-A|<8,只要x-x。<x,且x≥0,而x≥0可用x-x|≤x,保证.故取8=minx,,x,则当0<-x<时,必有Vx-/x<lim Vx = /x.因此X→Xo
0 0 0 4 0 lim . x x x x x 例 证明:当 时, 证: 0 0 0 ( ) x x f x A x x x x 0 0 1 x x x 0 0 0 0 0 , ( ) , , 0 0 . f x A x x x x x x x x 要使 只要 且 ,而 可用 保证 故取 0 x x 0 0 lim x x x x 因此 min , , x x 0 0 0 则当0 x x 时,必有

(3).单侧极限:V例如,y=1-x1-x,x<0设 f(x)=[x2 +1, x≥0y=x?+1-证明lim f(x)= 1.0xx-0分x>0和x<0两种情况分别讨论x从左侧无限趋近x,记作x→x;x从右侧无限趋近x,记作x→x+
(3).单侧极限: 例如, lim ( ) 1. 1, 0 1 , 0 ( ) 0 2 f x x x x x f x x 证明 设 分x 0和x 0两种情况分别讨论 0 0 x x x x , ; 从左侧无限趋近 记作 0 0 x x x x , . 从右侧无限趋近 记作 y o x 1 y 1 x 1 2 y x