
复变函数(2) 对所有的正实数除 Z=0 外都发散此时,级数在复平面内除原点外处处发散例如,级数 1+z+22z2+..·+n"z"+当z≠0时,通项不趋于零,故级数发散(3)既存在使级数发散的正实数,也存在使级数收敛的正实数,设z=α时,级数收敛;Z=β时,级数发散.如图:山
11 (2) 对所有的正实数除 z=0 外都发散. 此时, 级数在复平面内除原点外处处发散. (3) 既存在使级数发散的正实数, 也存在使级数收 敛的正实数. 例如,级数 1+ z + 2 2 z 2 ++ n n z n + 当z 0时, 通项不趋于零, 设 z = 时,级数收敛; z = 时,级数发散. 如图: 故级数发散
复变函数收敛圆收敛半径RxβB0a8Z幂级数Cnz"白的收敛范围是以原点为中心的圆域n=0u
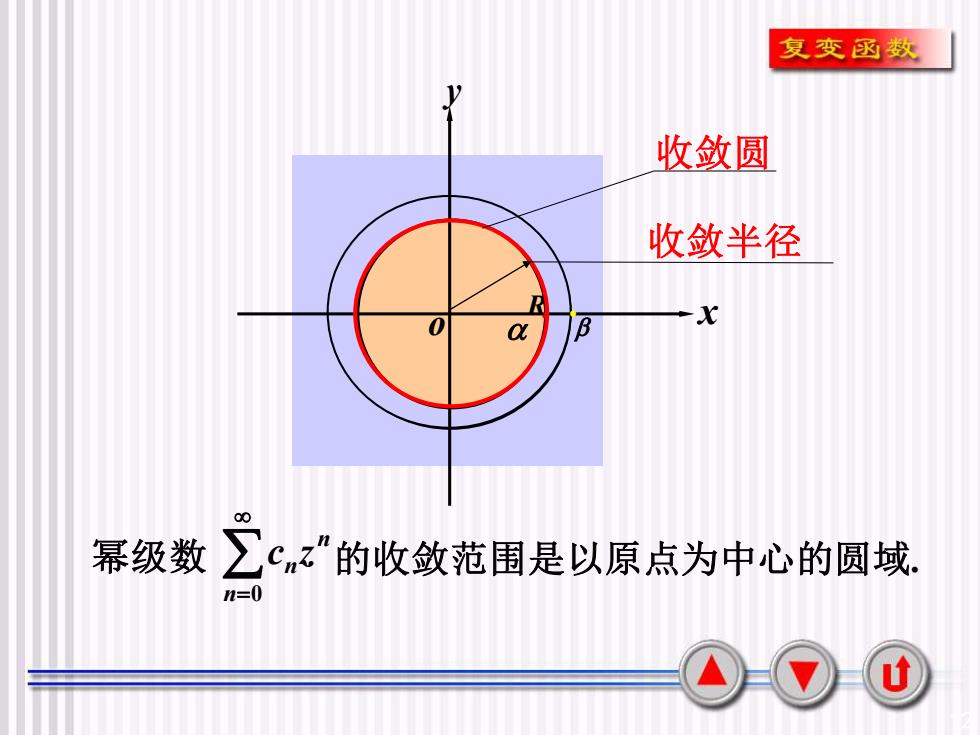
12 x y o . R. 收敛圆 收敛半径 幂级数 n=0 n n c z 的收敛范围是以原点为中心的圆域

复变函数8问题1:幂级数C,(z一a)"的收敛范围是何区域?n=0答案:是以z=为中心的圆域问题2:幂级数在收敛圆周上的敛散性如何?注意在收敛圆周上是收敛还是发散,不能作出一般的结论,要对具体级数进行具体分析U
13 答案: 是以 z = a 为中心的圆域. 幂级数 = − 0 ( ) n n 问题1: cn z a 的收敛范围是何区域? 在收敛圆周上是收敛还是发散, 不能作出 一般的结论, 要对具体级数进行具体分析. 注意 问题2: 幂级数在收敛圆周上的敛散性如何?