
复变函数第八章Fourier变换Recall:周期函数在一定条件下可以展开为Fourier级数:但全直线上的非周期函数不能有Fourier表示;引进类似于Fourier级数的Fourier积分(周期趋于无穷时的极限形式u
第八章 Fourier变换 Recall: 周期函数在一定条件下可以展开为Fourier级 数;但全直线上的非周期函数不能有Fourier 表示;引进类似于Fourier级数的Fourier积分 (周期趋于无穷时的极限形式)
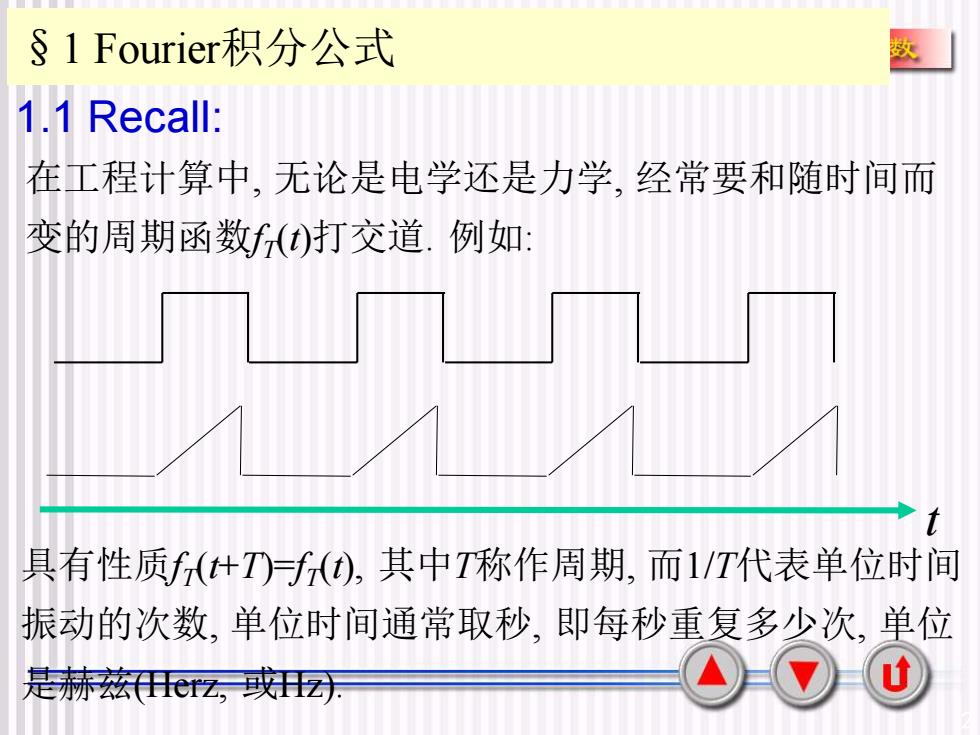
S1Fourier积分公式1.1 Recall:在工程计算中,无论是电学还是力学,经常要和随时间而变的周期函数f(t)打交道.例如:具有性质f(计T)=f(t),其中T称作周期,而1/T代表单位时间振动的次数,单位时间通常取秒,即每秒重复多少次,单位U是赫兹(llerz,或llz)
2 §1 Fourier积分公式 1.1 Recall: 在工程计算中, 无论是电学还是力学, 经常要和随时间而 变的周期函数fT (t)打交道. 例如: 具有性质fT (t+T)=fT (t), 其中T称作周期, 而1/T代表单位时间 振动的次数, 单位时间通常取秒, 即每秒重复多少次, 单位 是赫兹(Herz, 或Hz). t
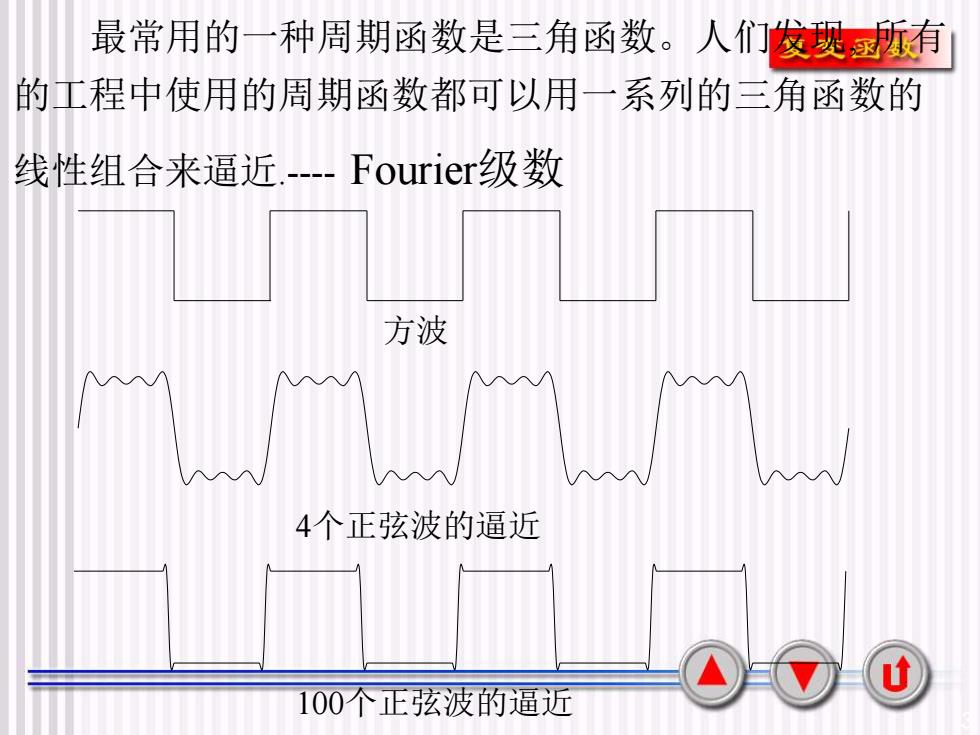
最常用的一种周期函数是三角函数。人们发现逐所有的工程中使用的周期函数都可以用一系列的三角函数的线性组合来逼近.---Fourier级数方波4个正弦波的逼近U100个正弦波的逼近
3 最常用的一种周期函数是三角函数。人们发现, 所有 的工程中使用的周期函数都可以用一系列的三角函数的 线性组合来逼近.- Fourier级数 方波 4个正弦波的逼近 100个正弦波的逼近

研究周期函数实际上只须研究其中的变函周期内的情况即可,通常研究在闭区间[-T/2,T/21内函数变化的情况.上满足f(t)为T一周期函数,在2°2Dirichlet条件:·f(t)连续或仅有有限个第一类间断点;·(t)仅有有限个极值点则f(t)可展开为Fourier级数,且在连续点t处成立:f. (t)= % + (a, cosnot + b, sinnotu
4 ( ) 0 1 ( ) , 2 2 Dirichlet ( ) ( ) ( ) Fourier ( ) cos sin 2 T T T T T n n n T T f t T f t f t f t t a f t a n t b n t = − − • • = + + 为 周期函数,在 上满足 条件: 连续或仅有有限个第一类间断点; 仅有有限个极值点 则 可展开为 级数,且在连续点 处成立: 研究周期函数实际上只须研究其中的一个周 期内的情况即可, 通常研究在闭区间[−T/2,T/2]内 函数变化的情况

其中=2元/T,复变函数2CT/2f- (t)cosnotdt (n = O,1, 2,...)a,T二n-T/22T/2b.fr (t)sinnotdt (n = 1,2, ..)1Fn-T/2在间断点t处成立:8f(t + O)+ f (t - 0)aoZ(cosnot + b, sinnota.十22n=1引进复数形式:inotinotinotinote+eeecos not, sin not22iU
5 ( ) ( ) 2 2 2 2 2 , 2 ( )cos 0,1,2, 2 ( )sin 1,2, T n T T T n T T T a f t n tdt n T b f t n tdt n T − − = = = = = 其中 ( ) 0 1 ( 0) ( 0) cos sin 2 2 T T n n n t f t f t a a n t b n t = + + − = + + 在间断点 处成立: 引进复数形式: i e e n t e e n t i n t i n t i n t i n t 2 ,sin 2 cos − − − = + =