《复变函数与积分变换》课程教学资源（PPT课件）第三章 复变函数的积分 3.0 习题课

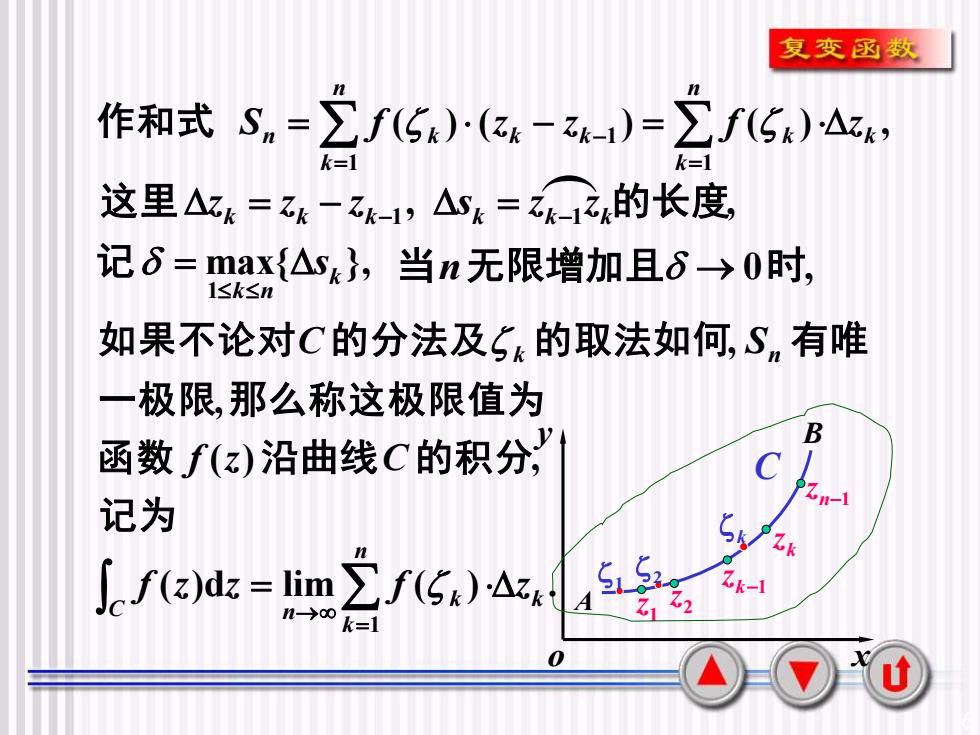
复变函数作和式 S,=f(S)·(zk=zk-1)=f(5k)△zk)k=1k=1这里△z= zZk-1，ASk=zk的长度,记s=max[△s，当n无限增加且S→0时,1≤k≤n如果不论对C的分法及的取法如何,S.有唯一极限，那么称这极限值为B函数f(z)沿曲线C的积分;C1Zzn-1记为CHTS. S?Zf(Sk)AzkZk-1(Cf(z)dz = lim22Zn-→>0k=10U

6 ( ) ( ) ( ) , 1 1 1 k n k k n k n k k k S =  f  z − z =  f z = = 作和式  −  o x y A B n−1 z k z k−1 z 2 z 1 z k  C 1  2 max{ }, 1 k k n = s   记 , , 这里zk = zk − zk−1 sk = zk−1 zk的长度 当n无限增加且 → 0时, ( ) , , , 记 为 函 数 沿曲线 的积分 一极限 那么称这极限值为 如果不论对 的分法及 的取法如何 有 唯 f z C C  k Sn ( )d lim ( ) . 1 k n k k C n f z z =  f z  = → 

复变函数3.积分存在的条件及计算（1）化成线积分设 f(z)=u(x,y)+iv(x,y)沿逐段光滑的曲线C连续,则积分cf(z)dz 存在,且[cf(z)dz= Ju(x,y)dx- v(x, y)dy +ij.(x,y)dx+u(x,y)dy.（2）用参数方程将积分化成定积分设简单光滑曲线C的参数方程是z = z(t) = x(t)+iy(t)(a≤t≤b)则Jc f(z)dz = J"f[z(t)] z'(t)dt.u

7 3.积分存在的条件及计算 （1）化成线积分 连续 则积分 存在 且 设 沿逐段光滑的曲线 , ( )d , ( ) ( , ) ( , )  = + C f z z f z u x y iv x y C    = − + + C C C f (z)dz u(x, y)dx v(x, y)dy i v(x, y)dx u(x, y)dy. （2）用参数方程将积分化成定积分 设简单光滑曲线C 的参数方程是 z = z(t) = x(t) + iy(t) (a  t  b) f (z)dz f[z(t)] z (t)dt. C b a =   则  

复变函数4.积分的性质设 f(z),g(z)沿曲线C连续(1) Jc f(z)dz =-Jc-(z)dz;(2) (_kf(z)dz = k cf(z)dz; ；(k为常数)(3) ([f(z)± g(z)dz = c f(z)dz± fcg(z)dz;(4)设C由C1,C,连结而成,则Jc f(z)dz = Jc, f(z)dz + Jc, F(z)dz;(5) 设曲线C的长度为L,函数 f(z)在C 上满足[cf(z)dz ≤ Jclf(z)ds ≤ML.f(z)≤M,那末U

8 4. 积分的性质 (1) ( )d ( )d ;  = − − C C f z z f z z (2) kf (z)dz k f (z)dz; (k为常数) C C = (3) [ ( ) ( )]d ( )d ( )d ;     =  C C C f z g z z f z z g z z 设 f (z), g(z)沿曲线C连续.    = + C C C f z z f z z f z z C C C 1 2 ( )d ( )d ( )d ; (4) , , 设 由 1 2连结而成 则      C C f z M f z z f z s ML C L f z C ( ) , ( )d ( )d . (5) , ( ) 那末 设曲线 的长度为 函数 在 上满足

复变函数5.柯西一古萨基本定理（柯西积分定理如果函数,f(z)在单连通域B内处处解析那末函数f(z)沿B内的任何一条封闭曲线C的积分为零：f,f(z)dz = 0.定理1如果函数f(z)在单连通域B内处处解析，那末积分f(z)dz与连结起点及终点的路线C无关u

9 5. 柯西－古萨基本定理(柯西积分定理) . , ( )d ( ) 线 无 关 析 那末积分 与连结起点及终点的路 定理1 如果函数 在单连通域 内处处解 C f z z f z B C : ( )d 0. ( ) ( ) ,  = c f z z f z B C f z B 的积分为零 那末函数 沿 内的任何一条封闭曲线 如果函数 在单连通域 内处处解析

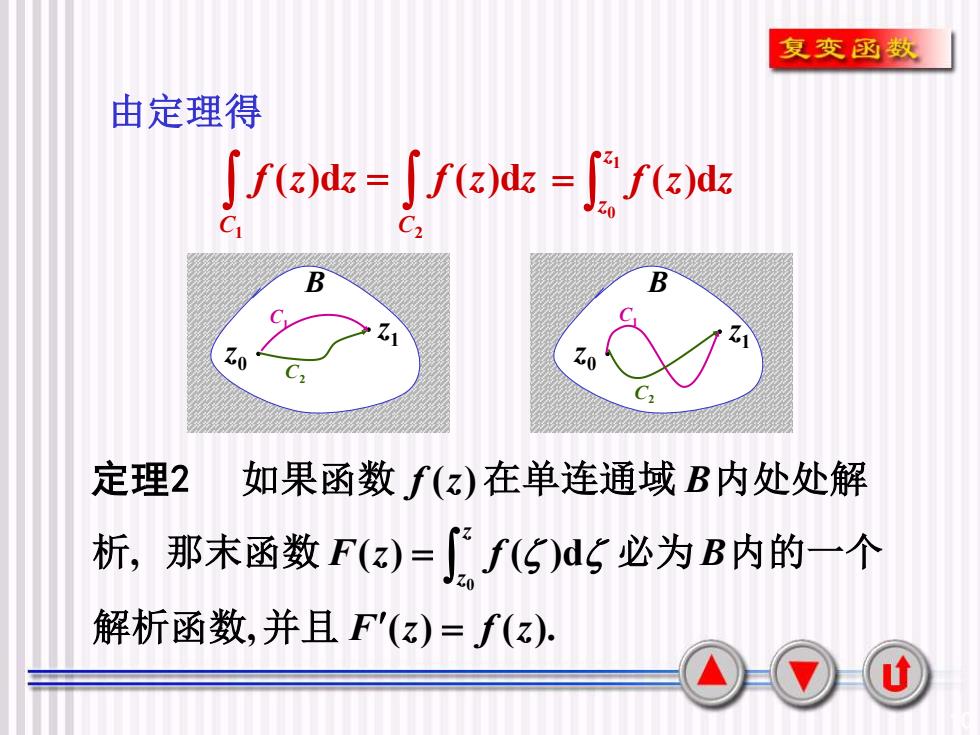
复变函数由定理得[(z)dz =[ f(z)dz =[" f(z)dzCC2BBCZ1Z1Zo10C2C2定理2如果函数 f(z)在单连通域B内处处解析，那末函数 F(z)=（f()d 必为B内的一个解析函数,并且 F(z)= f(z)u

10 , ( ) ( ). , ( ) ( )d ( ) 0 F z f z F z f B f z B z z  = =  解析函数 并且 析 那末函数 必为 内的一个 如果函数 在单连通域 内处处解   定理2 由定理得   = 1 2 ( )d ( )d C C f z z f z z  = 1 0 ( )d z z f z z B B  0 z 1 z  0 z 1 z C1 C2 C1 C2