
方法3.三次积分法 21(x,y)≤z≤22(x,y) 设区1a功心4g0 a≤x≤b 利用投影法结果,把二重积分化成二次积分即得 f(x.v.)dv =dsfc地 投影法 ,e动a=dd
山东农业大学 高等数学 主讲人:苏本堂 投影法 方法3. 三次积分法 设区域 : 利用投影法结果 , a x b y x y y x x y D ( ) ( ) ( , ) : 1 2 ( , ) ( , ) 1 2 z x y z z x y 把二重积分化成二次积分即得: = ( , ) ( , ) 2 1 d d ( , , )d z x y D z x y x y f x y z z ( , ) ( , ) 2 1 ( , , )d z x y z x y f x y z z ( ) ( ) 2 1 d y x y x y = b a dx

方本 小结:三重积分的计算方法 方法1.“先一后二” nx,yaa-,ddyfxg=d: 方法2.“先二后一” dv-d-f.dxdy 方法3.“三次积分” 瓜xd-dd: 三种方法各有特点,具体计算时应根据 被积函数及积分域的特点灵活选择
山东农业大学 高等数学 主讲人:苏本堂 小结: 三重积分的计算方法 方法1. “先一后二” 方法2. “先二后一” 方法3. “三次积分” = ( , ) ( , ) 2 1 d d ( , , )d z x y D z x y x y f x y z z = DZ b a d z f (x, y,z)dxdy = ( , ) ( , ) ( ) ( ) 2 1 2 1 d d ( , , )d z x y z x y y x y x b a x y f x y z z 三种方法各有特点, 具体计算时应根据 被积函数及积分域的特点灵活选择

例1化三重积分1=∬f(x,y,z)dc山k为三 Ω 次积分,其中积分区域Ω为由曲面 z=x2+y2,y=x2,y=1,z=0 所围成的空间闭区域。 解 2:0≤z≤x2+y2, x2≤y≤1,-1≤x≤1. 0.s I=处fx,z)k 00.250.50.75
山东农业大学 高等数学 主讲人:苏本堂 例 1 化三重积分 I = f (x, y,z)dxdydz为三 次积分,其中 积分区域为由曲面 2 2 z = x + y , 2 y = x , y = 1, z = 0 所围成的空间闭区域. 1, 1 1. : 0 , 2 2 2 − + x y x z x y − + = 1 1 0 1 2 2 2 ( , , ) x y x I dx dy f x y z dz. 解

山东农业大 等数学 主讲人: 方本堂 例2化三重积分I=川fx,y,dd为三次积分 2:z=y与x+y=1,z=0所围成的区域 x+y=1 y y
山东农业大学 高等数学 主讲人:苏本堂 1 x+ y=1 y o z x 1 z=xy . : z = xy与 x + y =,z = 所围成的区域 例2 化三重积分 I f (x, y,z)dxdydz = 为三次积分
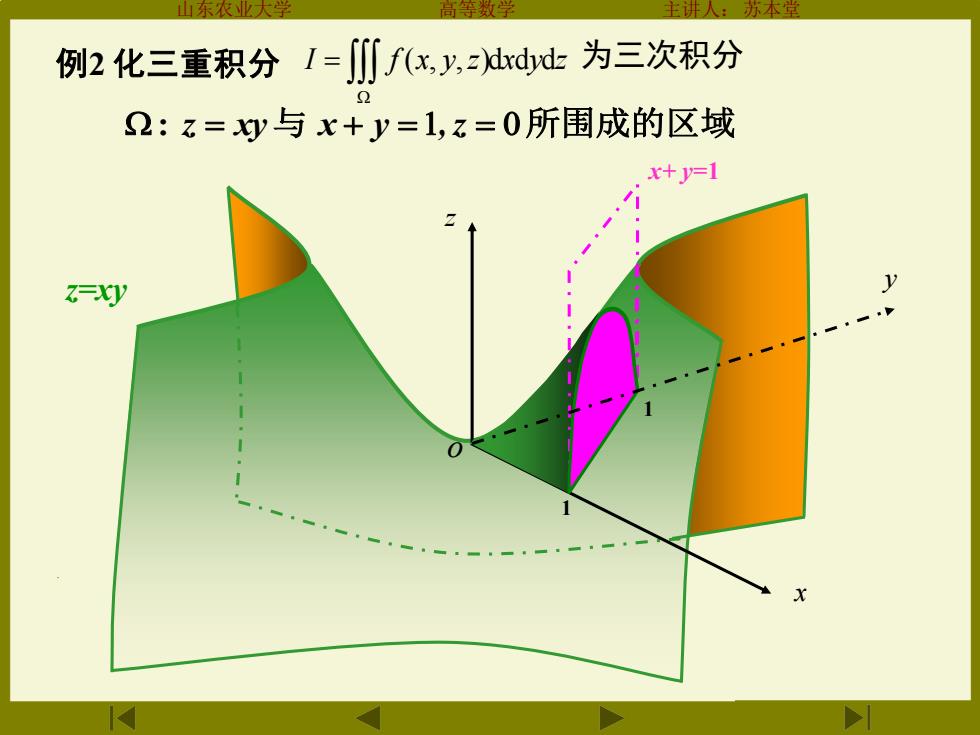
东农 主人 例2化三重积分I=川fx,y,灿dd为三次积分 2:z=y与x+y=1,z=0所围成的区域 x+y=1 y 2
山东农业大学 高等数学 主讲人:苏本堂 z =0 1 x+ y=1 o z x 1 y z=xy . : z = xy与 x + y =,z = 所围成的区域 例2 化三重积分 I f (x, y,z)dxdydz = 为三次积分