
第三章矩阵的初等变换与线性方程组 ·第一节矩阵的初等变换 ·第二节初等矩阵 ·第三节矩阵的秩 ·第四节线性方程组解的判别法
第三章矩阵的初等变换与线性方程组 • 第一节 矩阵的初等变换 • 第二节 初等矩阵 • 第三节 矩阵的秩 • 第四节 线性方程组解的判别法

第一节矩阵的初等变换 1、矩阵的初等变换 线性方程组的一般形式 41X1+122+.+41mXn 021火1+022火2+.+ a2nxn b2 0m11+0m2X2++0mXn=bm
第一节 矩阵的初等变换 线性方程组的一般形式 + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 1、 矩阵的 初等变换
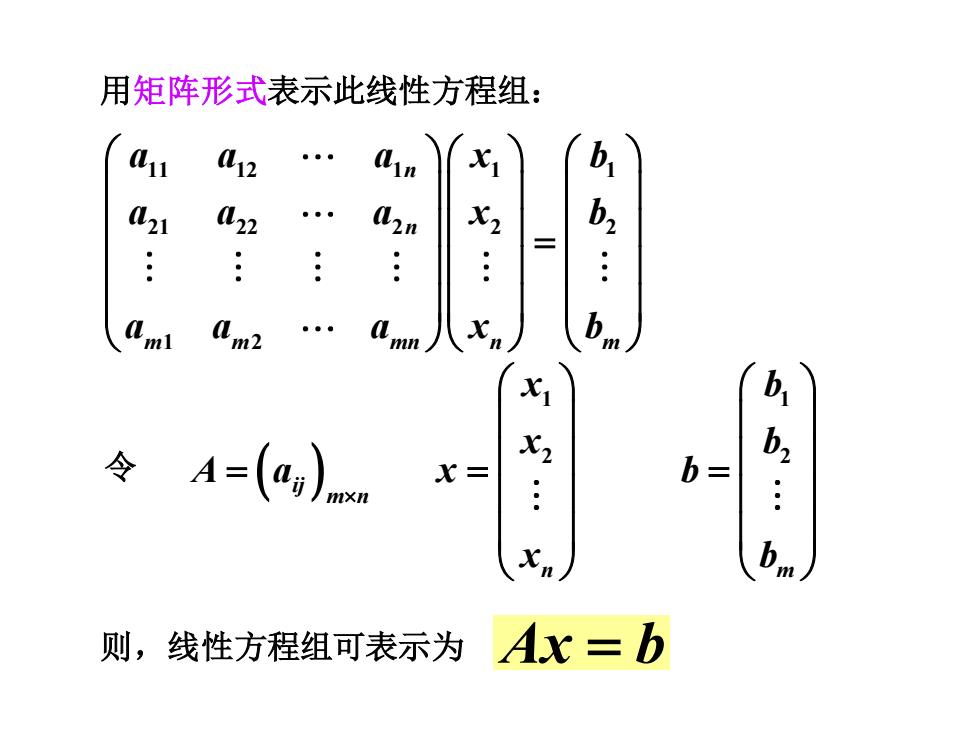
用矩阵形式表示此线性方程组: L11 12 b 21 22 02n X2 b, ● b mn 令A=(a)nn 七2 b2 X= b= Xn 则,线性方程组可表示为 Ax=b
用矩阵形式表示此线性方程组: 11 12 1 1 1 21 22 2 2 2 1 2 n n m m mn n m a a a x b a a a x b a a a x b = 令 1 2 n x x x x = 1 2 m b b b b = ( ij)m n A a = 则,线性方程组可表示为 Ax b =

如何解线性方程组?可以用消元法求解。 始终把方程组看作一个整体变形,用到如下三种变换: (1)交换方程次序; (2)以不等于0的数乘某个方程; (3)一个方程加上另一个方程的k倍. 由于三种变换都是可逆的,所以变换前的方程组与变 换后的方程组是同解的.故这三种变换是同解变换
如何解线性方程组? 可以用消元法求解。 始终把方程组看作一个整体变形,用到如下三种变换: (1)交换方程次序; (2)以不等于0的数乘某个方程; (3)一个方程加上另一个方程的k倍. 由于三种变换都是可逆的,所以变换前的方程组与变 换后的方程组是同解的.故这三种变换是同解变换.

因为在上述变换过程中,仅仅只对方程组的系数和常数 进行运算,未知量并未参与运算. 若记 l12 b B=(Ab)= l22 : ml mn 则对方程组的变换完全可以转换为 对矩阵B方程组的增广矩阵)的变换
若记 11 12 1 1 21 22 2 2 1 2 ( ) n n m m mn m a a a b a a a b B A b a a a b = = 则对方程组的变换完全可以转换为 对矩阵B(方程组的增广矩阵)的变换. 因为在上述变换过程中,仅仅只对方程组的系数和常数 进行运算,未知量并未参与运算.