
例2.求[(ax+b)"dx (m±-1).解:令u=ax+b,则du=adx,故m+1lumidu原式=「福m+1Q(ax + b)m+1 + Ca(m+1)注:当m=-1时dx=- inlax+bl+Cax+bC
例2. 求 解: 令 u a x b , 则 d u a d x , 故 原式 = m u u a d 1 a 1 u C m m 1 1 1 注: 当 时
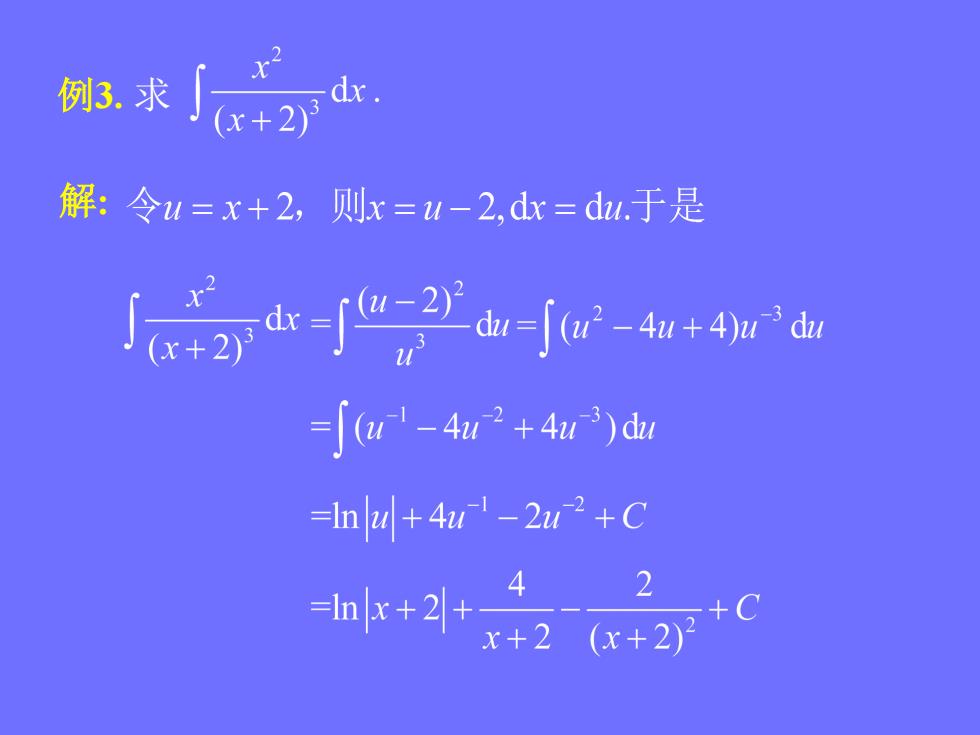
例3.求dx(x+2)解:令u=x+2,则x=u-2,dx= du.于是(u-2)2dx-du=[ (u? - 4u + 4)u-" dux+2)[(u-" - 4u-? + 4u-3)du=ln |ul + 4u-l - 2u-2 + C2=lnx+2|+x+2(x+2)
例3. 求 解:

dx想到公式例4.求dudxdx解:l+u= arctan u +u=则du=dxarctanu+caarctan(=)+ Ca
2 2 1 d 1 ( ) xax a 例4. 求 解 : , ax 令 u 则 x a u d 1 d 2 1 u d u a1 u C a arctan 1 想到公式 2 1 d uu a r c t a n u C ( ) xa

dx例5.求(a> 0).d()dxdx解:1-()2一=arcsin=+Cadu想到arcsinu+CJ [o(x)o'(x)dx = [ f(o(x)dp(x)(直接凑微分)
例5. 求 2 1 d u u 想到 a r c s i n u C 解: 2 d 1 ( ) x a x a f ( ( x) )d ( x) (直接凑微分) f [ ( x ) ] ( x )dx 2 d( ) 1 ( ) x a x a
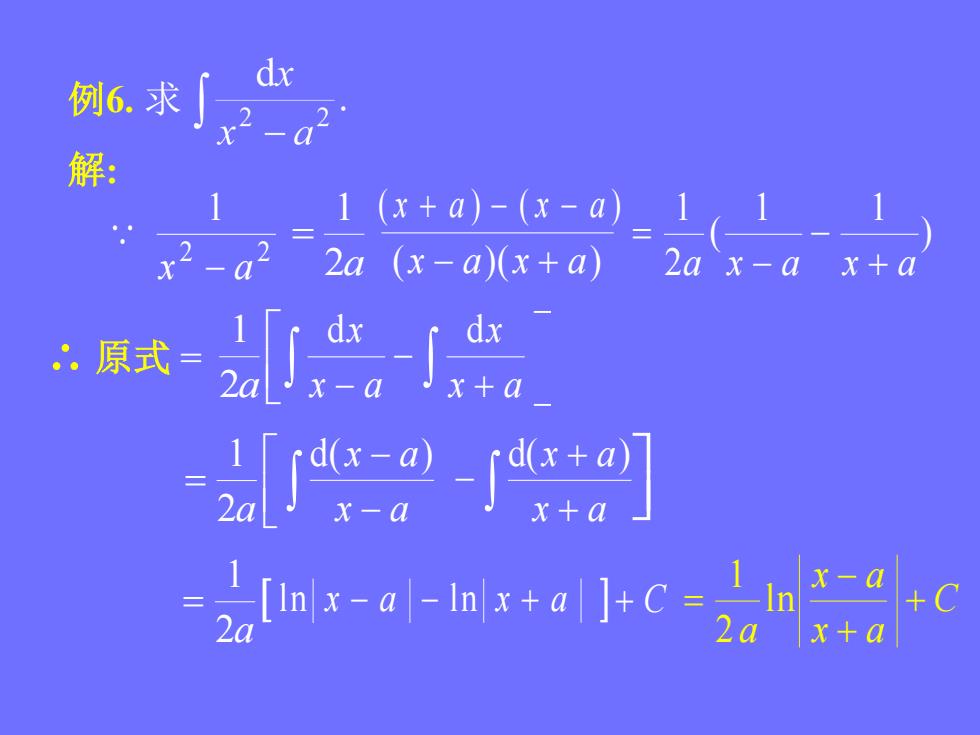
dx例6.求解:1(x+a)-(x-a) 1(2a(x-a)(x+a))2ax-ax+a[- da:原式c+a-2[-[ a]x+ax-a_[1n|x-a|-In|x+al ]+C =_in2ax+a
C x a x a a ln 2 1 例6. 求 解: 2 2 1 x a (x a)(x a) ( x a ) ( x a ) 2a 1 ) 1 1 ( 2 1 a x a x a ∴ 原式 = 2a 1 x a x x a dx d 2a 1 x a d(x a) 2a 1 ln x a l n x a C x a d(x a)