西安电子科技大学：《复变函数与场论》课程教学课件（讲义，2017）第24讲 初等函数映射

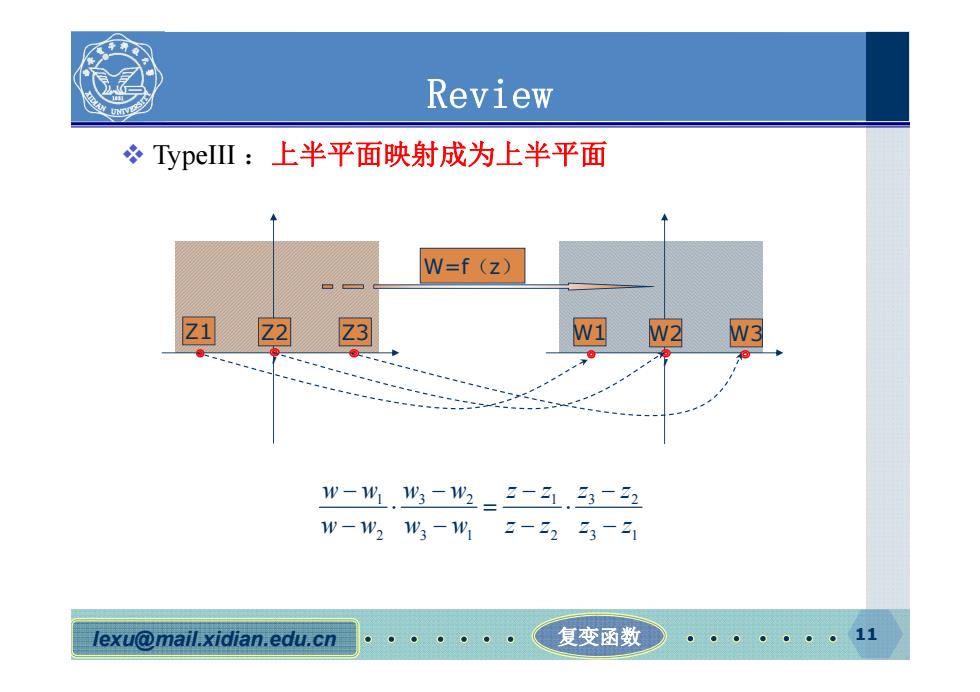
Review TypeIII：上半平面映射成为上半平面 W=f (z) 四孕 3 W3 w-.9虜-1业=2-.3-2 w-1w21W3-w12-2223-21 lexu@mail.xidian.edu.cn 复变函数 。。。。。。。11

lexu@mail.xidian.edu.cn 复变函数 11 Review  TypeIII ：上半平面映射成为上半平面 W=f（z） Z1 Z2 , Z3 W1 W2 , W3 1 1 3 2 32 2 3 1 23 1 ww zz ww zz ww w w zz z z         

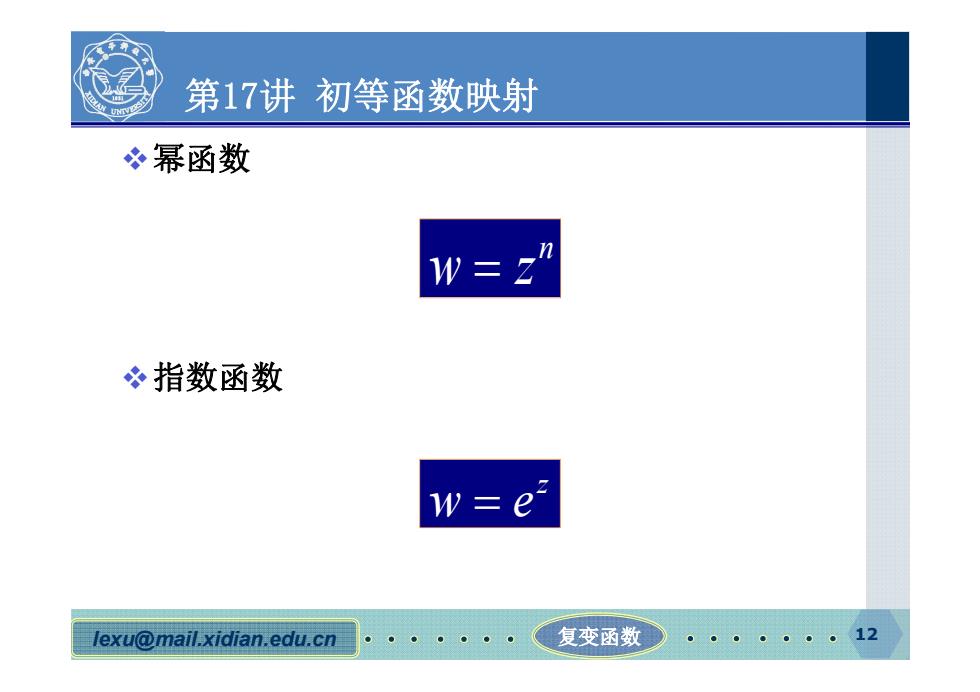
第17讲初等函数映射 必幂函数 n W=Z 指数函数 w=e Z lexu@mail.xidian.edu.cn 复变函数●。。。。。。。12

lexu@mail.xidian.edu.cn 复变函数 12 第17讲 初等函数映射 幂函数 指数函数 n w z  z w e 

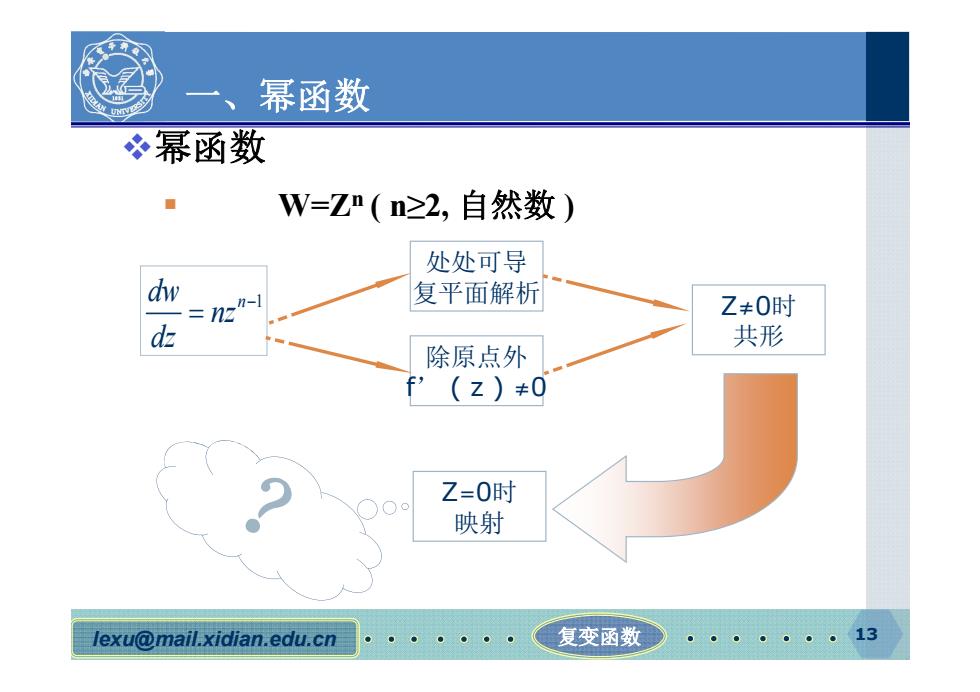
一、 幂函数 冬幂函数 W=Zn(n≥2，自然数) 处处可导 dw 复平面解析 Z+0时 dz 共形 除原点外 Z=0时 映射 lexu@mail.xidian.edu.cn 复变函数●

lexu@mail.xidian.edu.cn 复变函数 13 一、幂函数 幂函数  W=Zn ( n≥2, 自然数 ) dw n 1 nz dz   处处可导 复平面解析 除原点外 f’ ( z ) ≠0 Z≠0时 共形 Z=0时 映射

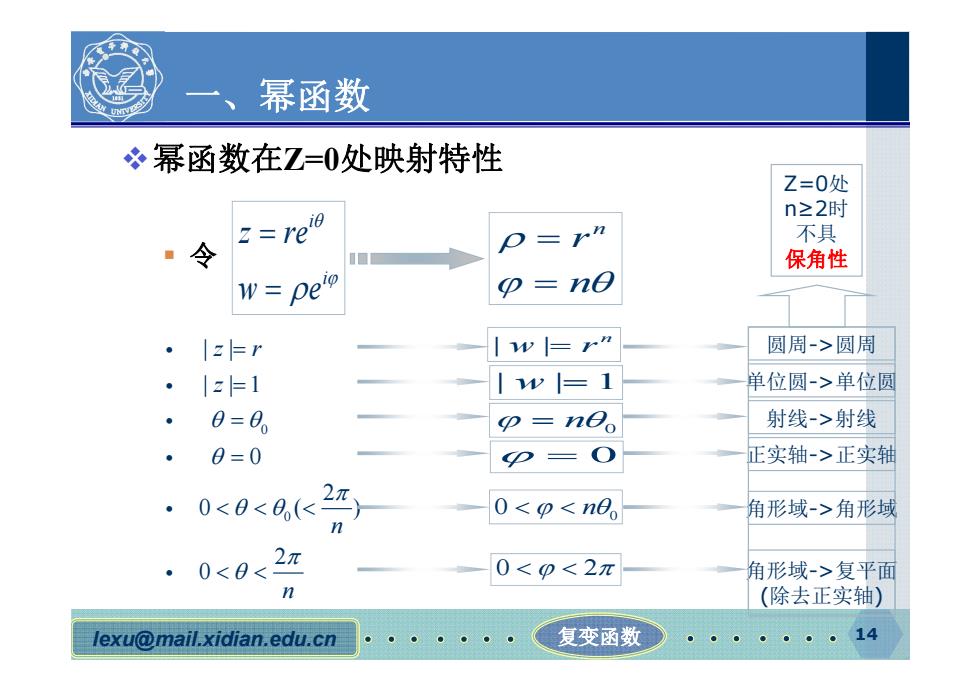
一、 幂函数 冬幂函数在Z=O处映射特性 Z=0处 n≥2时 2=1re9 =rn 不具 ·令 保角性 w=Delo =n0 ·z=r 圆周->圆周 ·|z=1 w 单位圆->单位圆 。 0=8 D= neo 射线->射线 0=0 D 正实轴->正实轴 2π 。 0<0<0(< 0<p<n8 角形域->角形域 0<0<2 0<p<2π 角形域->复平面 (除去正实轴) lexu@mail.xidian.edu.cn 复变函数 14

lexu@mail.xidian.edu.cn 复变函数 14 一、幂函数 幂函数在Z=0处映射特性  令 i i z re w e      n r n      0 0 | | | | 1 0 2 0 () 2 0 z r z n n                       | | w r  n 圆周->圆周 | |1 w    n0   0 0    n0 0 2     单位圆->单位圆 射线->射线 正实轴->正实轴 角形域->角形域 角形域->复平面 (除去正实轴) Z=0处 n≥2时 不具 保角性

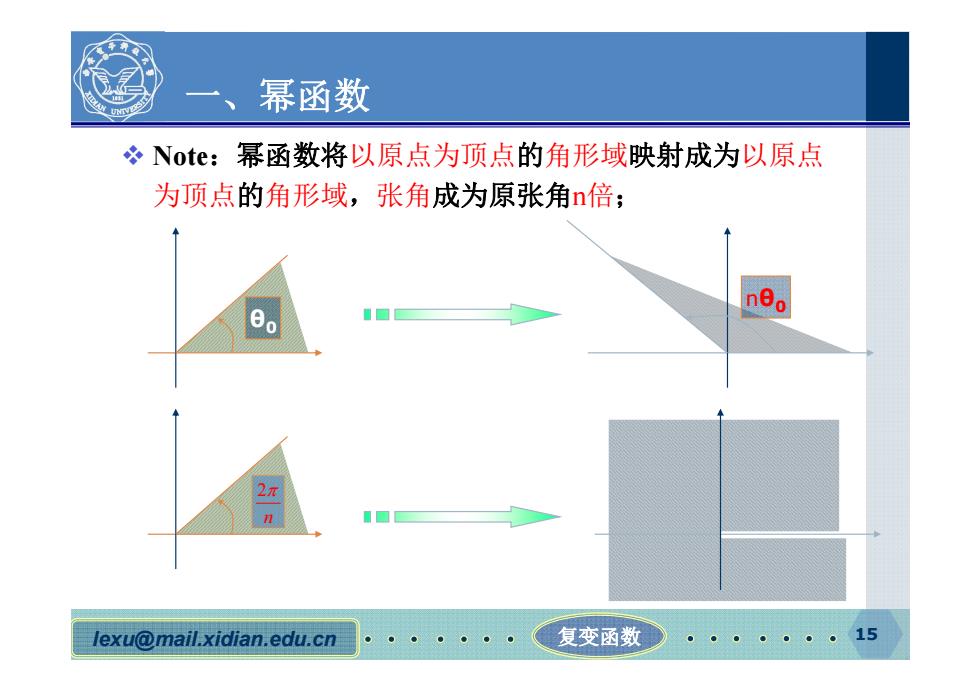
一、 幂函数 ÷Note:幂函数将以原点为顶点的角形域映射成为以原点 为顶点的角形域，张角成为原张角n倍； 2元 lexu@mail.xidian.edu.cn 复变函数● 15

lexu@mail.xidian.edu.cn 复变函数 15 一、幂函数  Note：幂函数将以原点为顶点的角形域映射成为以原点 为顶点的角形域，张角成为原张角n倍； θ0 nθ0 2 n 