Review W2 W 1W3 lexu@mail.xidian.edu.cn 复变函数D
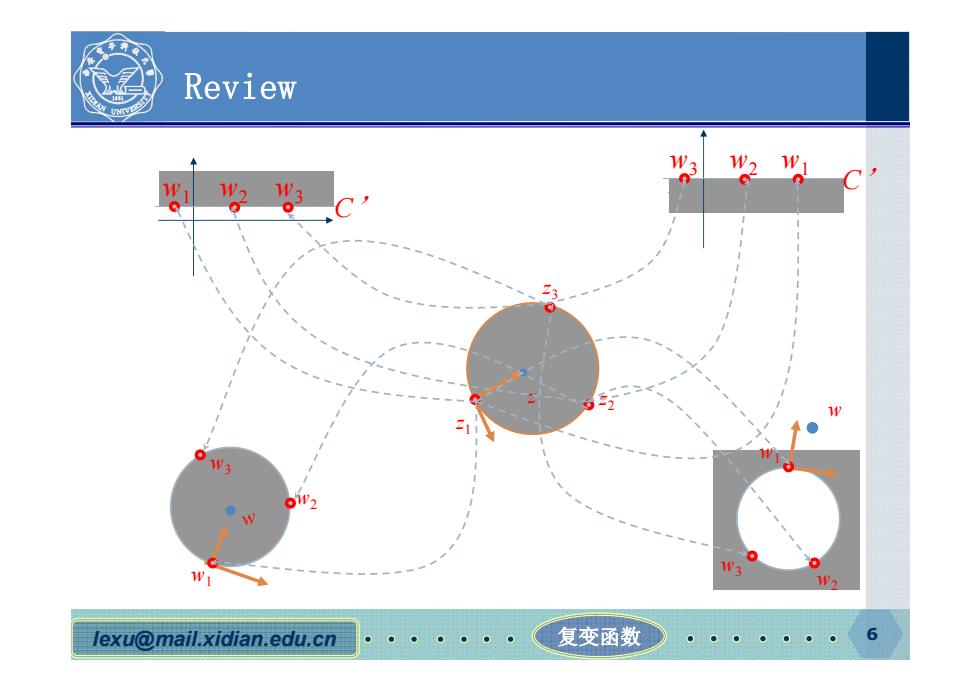
lexu@mail.xidian.edu.cn 复变函数 6 Review w1 w2 w3 C’ w3 w2 w1 C’ w1 w2 w3 z1 z2 z z3 w1 w2 w3 w
Review (①)二圆周上没有点映射成无穷远点 时,这二圆周的弧所围成的区域 映射成二圆弧所围成的区域: (I)二圆周上仅有一个点映射成无 穷远点时,这二圆周的弧所围成 的区域映射成一圆弧与一直线所 围成的区域: (III)二圆周一个交点映射成无穷远 点时,这二圆周的弧所围成的区 域映射成角形区域. lexu@mail.xidian.edu.cn 复变函数
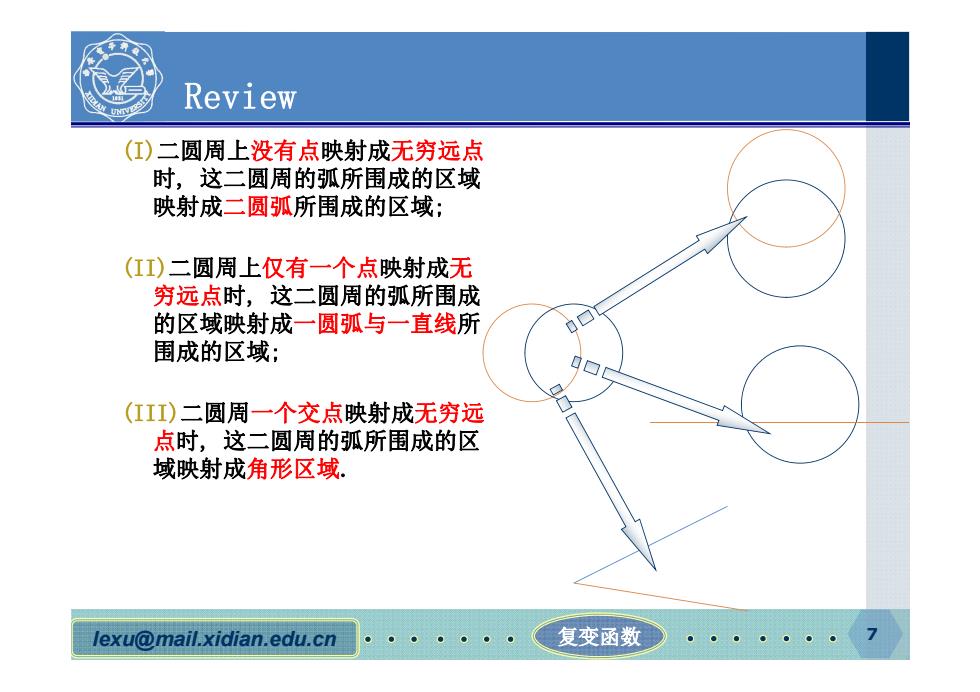
lexu@mail.xidian.edu.cn 复变函数 7 Review (I)二圆周上没有点映射成无穷远点 时, 这二圆周的弧所围成的区域 映射成二圆弧所围成的区域; (II)二圆周上仅有一个点映射成无 穷远点时, 这二圆周的弧所围成 的区域映射成一圆弧与一直线所 围成的区域; (III)二圆周一个交点映射成无穷远 点时, 这二圆周的弧所围成的区 域映射成角形区域
Review TypeI:上半平面映射成为单位圆 W=f (z) w10 Z1=入 W2=∞ Z2=入 z=九→1w=0 w=(二k z=九→> W=0 z∈Re→Iwl→lk=1→k=e9 w=(后re 入任意,且Im(入)>0 lexu@mail.xidian.edu.cn 复变函数 8
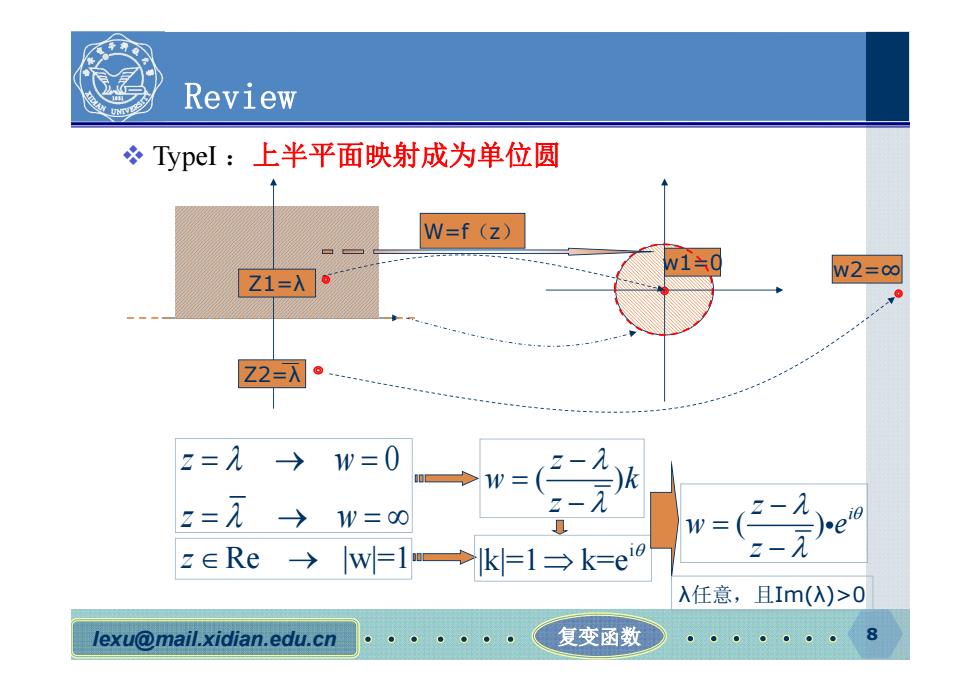
lexu@mail.xidian.edu.cn 复变函数 8 Review TypeI :上半平面映射成为单位圆 W=f(z) Z1=λ Z2=λ w1=0 w2=∞ z 0 w z w ( ) z w k z z Re |w|=1 i |k|=1 k=e ( ) z i w e z λ任意,且Im(λ)>0

Review 方法二采用唯一决定分式线形映射的条件求解1 w-w.w3-w=2-1.3-2 W-w2W3-9 2-2223-1 31=-1 "=1 p=-i(2- 2=0 w2=i Z+i 33-1 w3=-1 w2=i Z2=0 2●b- w3=-1 w1=1 Z1=1 Z3=1 lexu@mail.xidian.edu.cn 复变函数 9
lexu@mail.xidian.edu.cn 复变函数 9 Review [方法二 采用唯一决定分式线形映射的条件求解] 1 1 3 2 32 2 3 1 23 1 ww zz ww zz ww w w zz z z 1 2 3 1 0 1 z z z 1 2 3 1 -1 w w w i Z1=-1 Z2=0 w1=1 w2=i Z3=1 w3=-1 ( ) z i w i z i
Review TypeIⅡ:单位圆映射成为单位圆 W=f (z) W1=0 w2=00 Z1=a Z2=1/a 1w=0 = 2-)k z=0 → z-1/a 00 z=1/a 1W=00 -&k 1-@z w=(2- |z=1→ W=1i 1-@z k=1→k'=eo a任意,且a<1 lexu@mail.xidian.edu.cn 复变函数 。。。··。。10
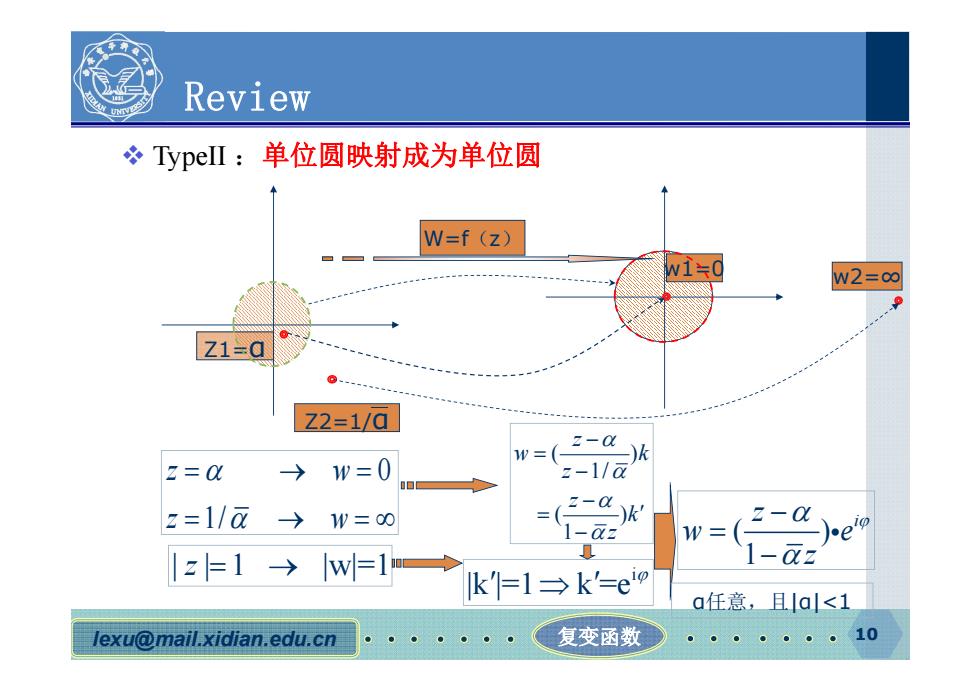
lexu@mail.xidian.edu.cn 复变函数 10 Review TypeII :单位圆映射成为单位圆 W=f(z) Z2=1/α w1=0 w2=∞ 0 1/ z w z w ( ) 1/ () 1 z w k z z k z | | z 1 |w|=1 i |k |=1 k =e ( ) 1z i w e z α任意,且|α|<1 Z1=α