《复变函数与积分变换》课程教学资源（PPT课件）第三章 复变函数的积分 3.4 第四节 原函数与不定积分

复变函数Z+4z于是 F(zz)-F()=f()ds,C+A7因为f(z)d5 =f(z)[ ds = f(z)Az,F(z+ △z)- F(z)所以-f(z)Az1Cz+zf(S)d5 - f(z)-12+4zAzJZKBzS[f() - f(z)]dsAzJzZou

6 于是 F(z + z) − F(z) = ( )d ,  z+z z f   =  z+z z 因为 f (z)d  z+z z f (z) d = f (z)z, B z K z + z  0 z •  ( ) ( ) ( ) f z z F z z F z −  +  − 所以 ( )d ( ) 1 f f z z z z z −  =  +   [ ( ) ( )]d 1 f f z z z z z −  =  +

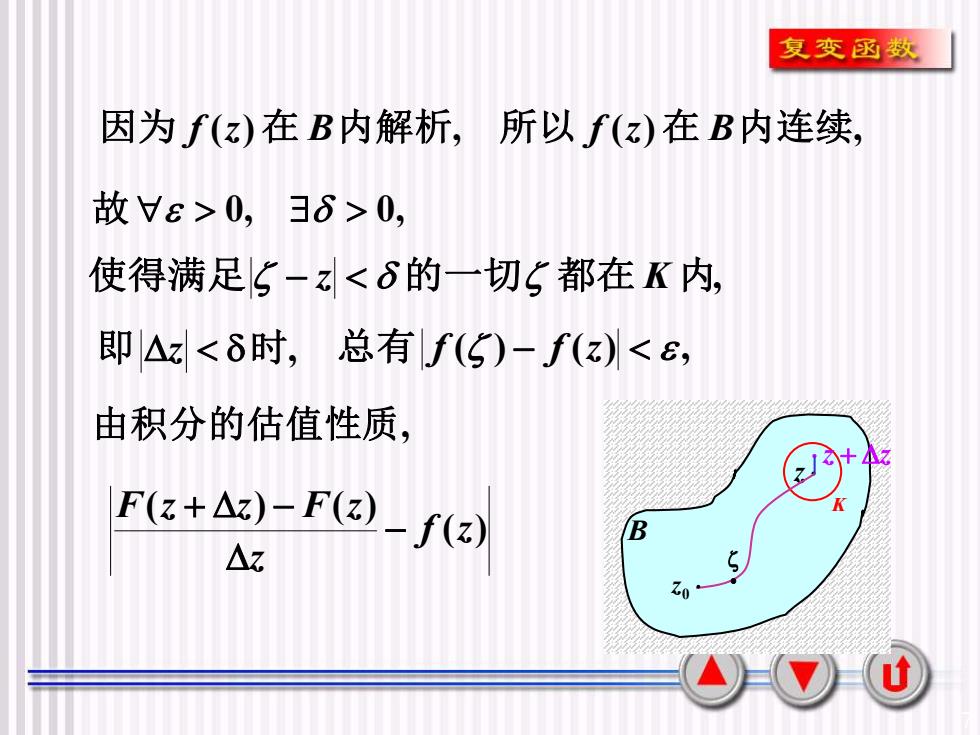
复变函数因为 f(z)在B内解析，所以 f(z)在B内连续故>0,>0,使得满足一z<的一切都在内即z<时，总有f()f(z)<,由积分的估值性质2+47F(z +△z) - F(z)K2- f(z)BAzSZou

7 B z K z + z  0 z •  因为 f (z)在 B内解析, 所以 f (z)在 B内连续, 故  0,   0, 使得满足 − z   的一切 都在 K 内, 即 z  时, 总有 f ( ) − f (z)   , 由积分的估值性质, ( ) ( ) ( ) f z z F z z F z −  +  −

复变函数F(z + △z)- F(z)Cz+Azf(z)[f(S) -f(z)]d-AzAz.Cz+Az≤f(S)-f(z)IdS≤.8.4z=8.AzJzAzF(z +△z)- F(z)于是limf(z)= 0,Azz-→0即[证毕]F'(z) = f(z)此定理与微积分学中的对变上限积分的求导定理完全类似U

8 ( ) ( ) ( ) f z z F z z F z −  +  − [ ( ) ( )]d 1 f f z z z z z −  =  + | ( ) ( )| d 1 f f z z z z z −    + . 1     =    z z ( ) 0, ( ) ( ) lim 0 − =  +  −  → f z z F z z F z z 于是即 F(z) = f (z). 此定理与微积分学中的对变上限积分的求导 定理完全类似. [证毕]