《概率论与数理统计》课程教学课件（PPT讲稿）第03章 多维随机变量及其分布 3.5 两个随机变量的函数的分布

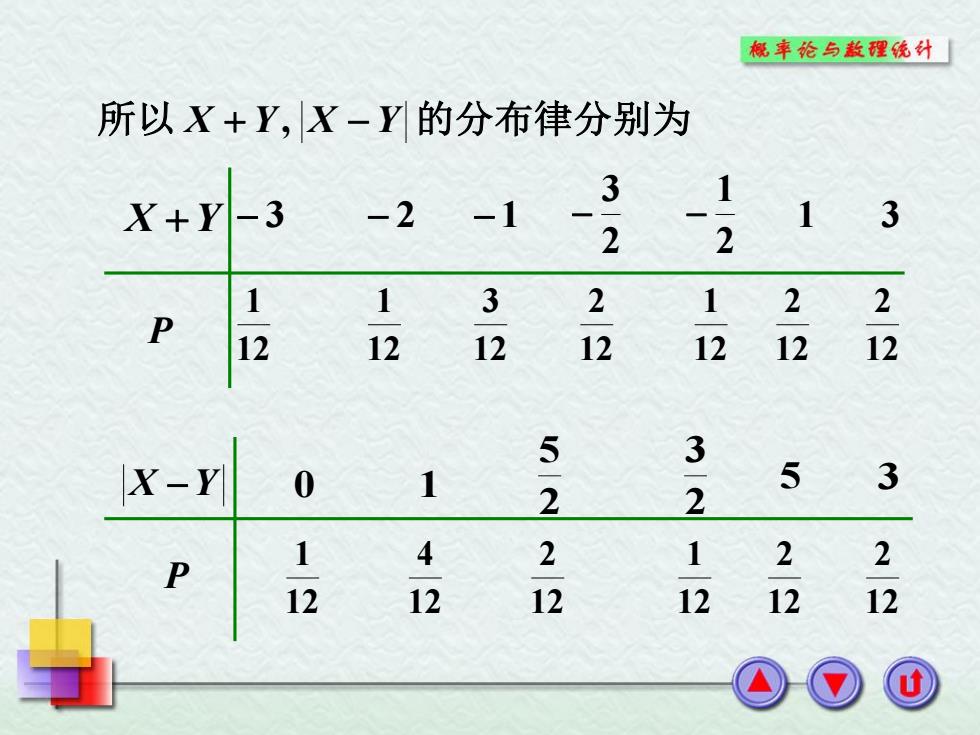
概率论与赦理统计 所以X+Y,X-Y的分布律分别为 X+Y -3 1 -2-1 3 1 3 2 1-12 1-12 3 2 1 2 P 12 12 12 12 12 X-Y 0 1 5-2 3-2 5 3 1 4 2 1 2 2 P 12 12 12 12 12 12

X Y P  3  2  1 2 3  2 1  1 3 12 1 12 1 12 3 12 2 12 1 12 2 12 2 X Y P 0 1 2 5 2 3 5 3 12 4 12 1 12 2 12 1 12 2 12 2 所以 X  Y, X Y 的分布律分别为

概率论与数理统外「 结论 若二维离散型随机变量的联合分布律为 P{X=x,Y=yj}=P,i,j=1,2,. 则随机变量函数Z=(X,Y)的分布律为 P(Z==P(g(X,Y)=) =∑Pgk=1,2, Zk=g(xiyi)

结论 若二维离散型随机变量的联合分布律为 { , } , , 1,2, P X x Y y p i j     i j ij 则随机变量函数Z  g(X,Y)的分布律为 { } { ( , ) } P Z z P g X Y z    k k ( ) 1,2, . k i j ij z g x y p k    

概率枪与散理统外】 例2设两个独立的随机变量X与Y的分布律为 X 3 Y 2 4 P 0.3 0.7 0.6 0.4 求随机变量Z=X+Y的分布律， 解因为X与Y相互独立，所以 P(X=xi,Y=y }=P(X=x)P(Y=y}, 2 4 得 1 0.18 0.12 30.42 0.28

例2 设两个独立的随机变量X 与Y 的分布律为 X PX 1 3 0.3 0.7 Y PY 2 4 0.6 0.4 求随机变量 Z=X+Y 的分布律. { , } { } { }, i j i j P X  x Y  y  P X  x P Y  y 得 Y X 2 4 1 3 0.18 0.12 0.42 0.28 解 因为 X 与 Y 相互独立, 所以

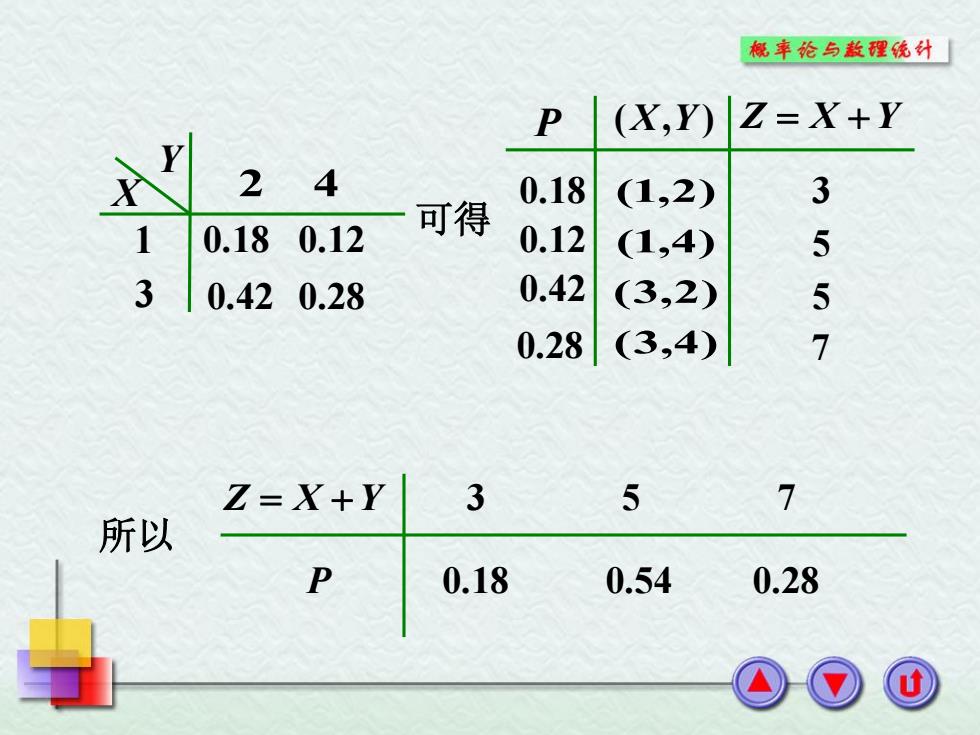
概率论与敖理统计「 P (X,Y) Z=X+Y X 24 0.18 (1,2) 3 可得 1 0.180.12 0.12 (1,4) 5 3 0.420.28 0.42 (3,2) 5 0.28 (3,4) 7 Z=X+Y 3 5 7 所以 P 0.18 0.54 0.28

可得 (X,Y ) (3,4) (3,2) (1,4) (1,2) P 0.18 0.12 0.42 0.28 Z  X Y 3 5 5 7 所以 Z  X Y P 3 5 7 0.18 0.54 0.28 Y X 2 4 1 3 0.18 0.12 0.42 0.28

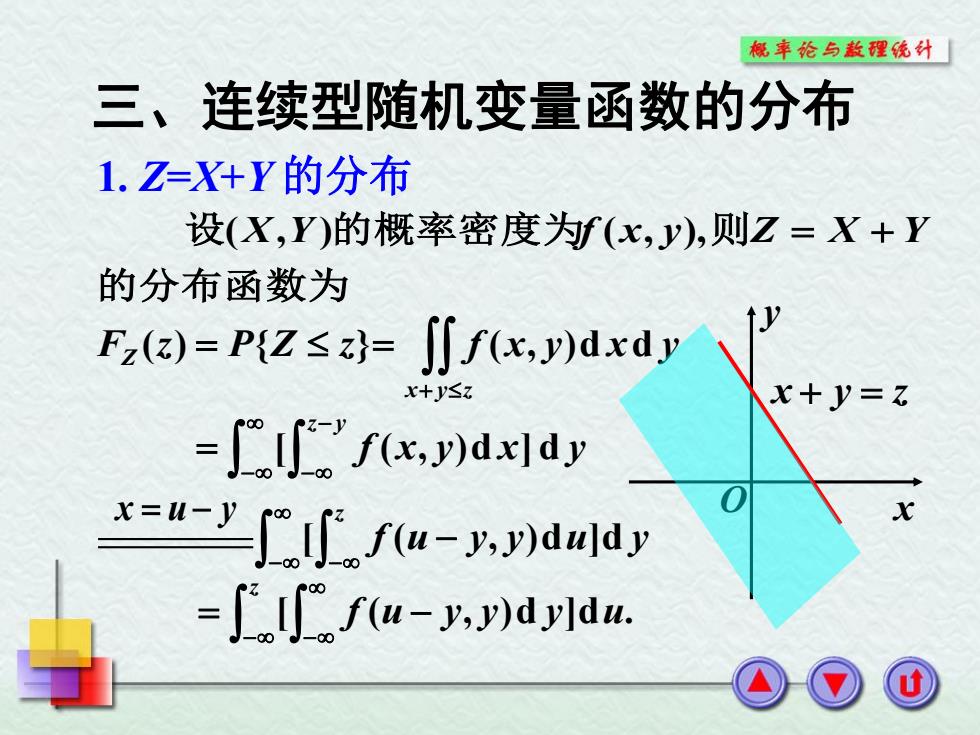
概率论与散理统外 三、连续型随机变量函数的分布 1.Z=X+Y的分布 设(X,Y)的概率密度为f(x,y),则Z=X+Y 的分布函数为 Fz(a)=P{Z≤z=∫∬fx,y)dxdy x+y≤z x+y=7 -f(x,y)dxlay xu-yfu-y.y)dndy =lf(u-y,y)dyldu

的分布函数为 设(X,Y )的概率密度为f (x, y),则Z  X  Y F (z) P{Z z} Z   f x y x y x y z ( , )d d     x y O x  y  z f x y x y z y [ ( , )d ] d        x  u  y f u y y u y z [ ( , )d ]d       [ f (u y, y)d y]du. z       三、连续型随机变量函数的分布 1. Z=X+Y 的分布