《概率论与数理统计》课程教学课件（PPT讲稿）第04章 随机变量的数字特征 4.2 方差

概率论与敖理统外 第二节方差 一、随机变量方差的概念及性质 二、重要概率分布的方差 三、例题讲解 四、小结

一、随机变量方差的概念及性质 三、例题讲解 二、重要概率分布的方差 四、小结 第二节 方 差

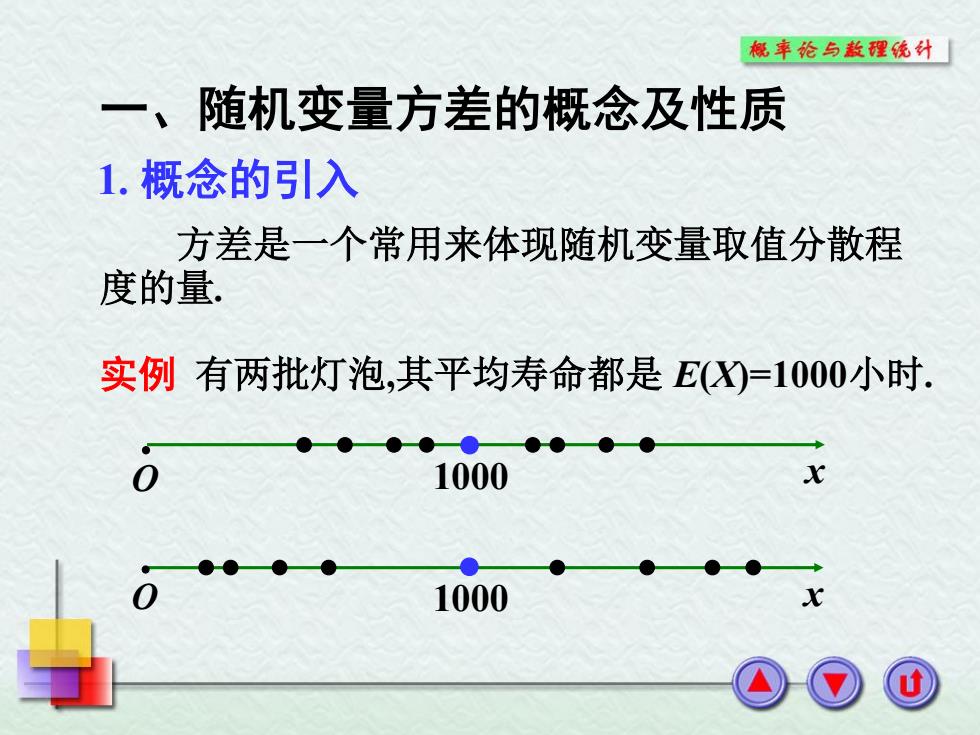
概率论与数理统外】 一、随机变量方差的概念及性质 1.概念的引入 方差是一个常用来体现随机变量取值分散程 度的量. 实例有两批灯泡，其平均寿命都是E)=1000小时 0 1000 ● 1000

1. 概念的引入 方差是一个常用来体现随机变量取值分散程 度的量. 实例 有两批灯泡,其平均寿命都是 E(X)=1000小时.  O x          O x          1000  1000 一、随机变量方差的概念及性质

概率论与敖理统计 2.方差的定义 设X是一个随机变量，若E{LX-E(X)}存在， 则称E{IX-E(X)]}为X的方差，记为D(X)或 Var(X),即 D(X)=Var(X)=EX-E(X). 称√D(X)为标准差或均方差，记为o(X)

( ) , ( ). ( ) Var( ) {[ ( )] }. Var( ), {[ ( ) ] } , ( ) , {[ ( )] } , 2 2 2 D X σ X D X X E X E X X E X E X X D X X E X E X 称 为标准差或均方差 记 为 即 则 称 为 的方差 记 为 或 设 是一个随机变量 若 存 在      2. 方差的定义

概率伦与散理统针」 3.方差的意义 方差是一个常用来体现随机变量X取值分散 程度的量如果D)值大，表示X取值分散程度大， E)的代表性差；而如果D(X)值小，则表示X的 取值比较集中，以E()作为随机变量的代表性好

方差是一个常用来体现随机变量X取值分散 程度的量.如果D(X)值大, 表示X 取值分散程度大, E(X)的代表性差;而如果D(X) 值小, 则表示X 的 取值比较集中,以E(X)作为随机变量的代表性好. 3. 方差的意义

概率论与散理统计 4.随机变量方差的计算 ()利用定义计算 离散型随机变量的方差 D(X)=I:-E(X)FP 其中P{X=x}=P,k=1,2,.是X的分布律 连续型随机变量的方差 D(X)=Ix-E(X)f(x)dx, 其中f(x)为X的概率密度

离散型随机变量的方差 ( ) [ ( )] , 1 2 k k k D X  x E X p     连续型随机变量的方差 ( ) [ ( )] ( )d , 2 D X x E X f x x      4. 随机变量方差的计算 (1) 利用定义计算 其中 f (x)为X的概率密度. { } , 1,2, . 其中P X x p k X    k k 是 的分布律