《概率论与数理统计》课程教学课件（PPT讲稿）第06章 样本及抽样分布 6.3 统计量及其分布

概率论与敖理统外 第二节 抽样分布 一、基本概念 二、常见分布 三、小结

第二节 抽样分布 一、基本概念 二、常见分布 三、小结

概率论与数理统外「 一、基本概念 1.统计量的定义 设X1,X2,Xn是来自总体X的一个样本， 8(X1,X2,.,Xn)是X1,X2,Xn的函数，若g中 不含未知参数，则称g(X1,X2,Xn)是一个统 计量. 设x,2,xn是相应于样本X1,X2,Xm 的样本值，则称g(化1，x2,.,xn)是g(X1,X2,Xn) 的观察值

一、基本概念 1. 统计量的定义 , 1 2 1 2 1 2 1 2 , , , , ( , , , ) , , , , ( , , , ) . n n n n X X X X g X X X X X X g g X X X 设 是来自总体 的一个样本 是 的函数 若 中 不含未知参数 则称 是一个统 计量 1 2 1 2 1 2 1 2 , , , , , , , ( , , , ) ( , , , ) . n n n n x x x X X X g x x x g X X X 设 是相应于样本 的样本值 则称 是 的观察值

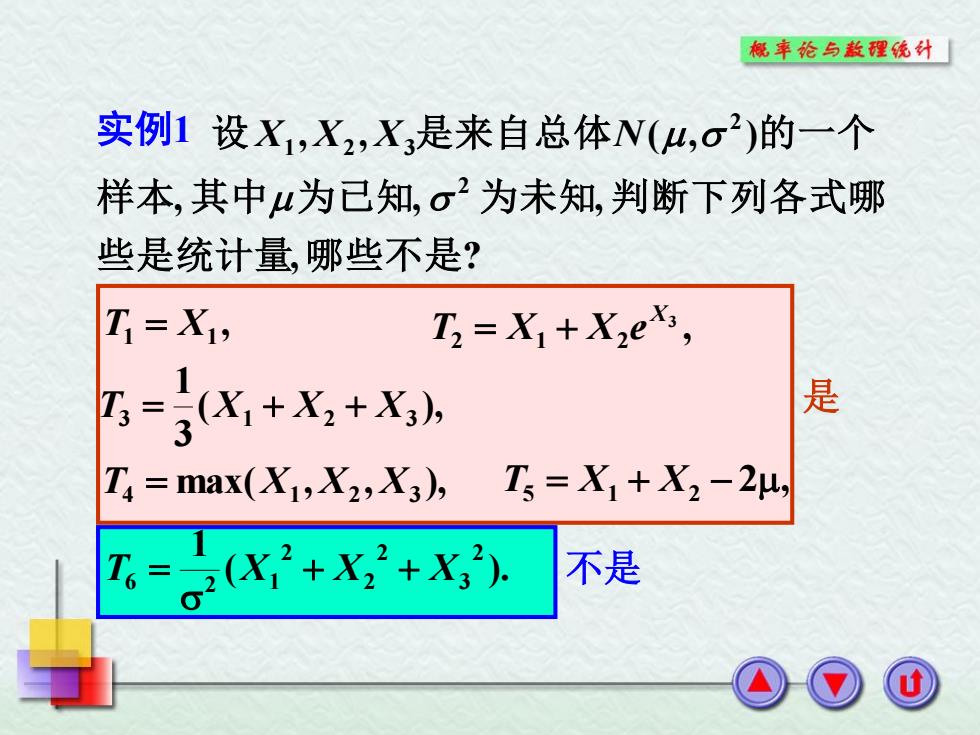
概率论与散理统外 实例1设X1,X2,X3是来自总体N(4,σ)的一个 样本，其中μ为已知，σ2为未知，判断下列各式哪 些是统计量，哪些不是？ T1=X, T3=X1+X2e, 3-时g+X+ 是 T4=max(X,X2,X3),T5=X+X2-2μ， =。X++Xi 不是

, ? , , , , , ( , ) 2 2 1 2 3 些是统计量 哪些不是 样 本 其 中 为已知 为未知 判断下列各式哪 设 是来自总体 的一个   X X X N   , T1  X1 , 3 2 1 2 X T  X  X e ( ), 3 1 T3  X1  X2  X3 max( , , ), T4  X1 X2 X3 2 , T5  X1  X2   ( ). 1 2 3 2 2 2 T6 2 X1  X  X   是 不是 实例1

概率论与散理统外「 2.几个常用统计量的定义 设X,X2,.,X,是来自总体X的一个样本， 七1,2，xn是这一样本的观察值 (1)样本平均值 X=>X n i=1 其观察 直x=x i=1 (2)样本方差 -2-②-

2. 几个常用统计量的定义 1 2 1 2 , , , , , , , . n n X X X X x x x 设 是来自总体 的一个样本 是这一样本的观察值 (1)样本平均值 ; 1 1   n i Xi n X (2)样本方差     n i Xi X n S 1 2 2 ( ) 1 1 . 1 1 1 2 2           n i Xi nX n . 1 1   n i xi n 其观察值 x

概率论与散理统计「 其观察值 2-水{〔②-m (3)样本标准差 S=VS2= 其观察值

其观察值     n i xi x n s 1 2 2 ( ) 1 1 . 1 1 1 2 2           n i xi nx n (3)样本标准差   ; 1 1 1 2 2      n i Xi X n S S 其观察值 ( ) . 1 1 1 2     n i xi x n s