
概率论与散理统计 第五节 两个随机变量的函数的分布 一、问题的引入 二、离散型随机变量函数的分布 三、连续型随机变量函数的分布 四、小结
二、离散型随机变量函数的分布 三、连续型随机变量函数的分布 四、小结 一、问题的引入 第五节 两个随机变量的函数的分布

概率论与数理统外「 一、问题的引入 有一大群人,令X和Y分别表示一个人的 年龄和体重,Z表示该人的血压并且已知Z与 X,Y的函数关系Z=g(X,Y),如何通过X,Y的 分布确定Z的分布. 为了解决类似的问题下面 我们讨论随机变量函数的分布
. , ( , ), , , , , 分布确定 的分布 的函数关系 如何通过 的 年龄和体重 表示该人的血压 并且已知 与 有一大群人 令 和 分别表示一个人的 Z X Y Z g X Y X Y Z Z X Y 为了解决类似的问题下面 我们讨论随机变量函数的分布. 一、问题的引入
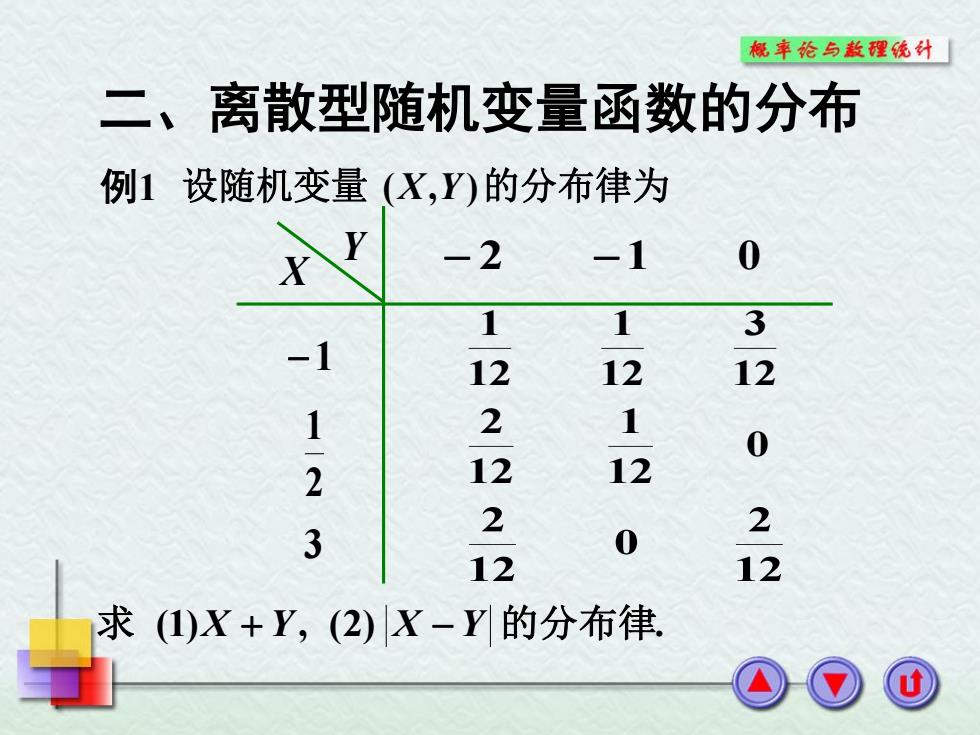
概率论与敖理统计 二、离散型随机变量函数的分布 例1设随机变量(X,)的分布律为 -2 -1 0 1 1 3 12 12 12 1 2 1 0 2 12 12 2 2 3 0 12 12 求(1)X+Y,(2)X-Y的分布律
二、离散型随机变量函数的分布 X Y 2 1 0 1 2 1 3 12 3 12 1 12 1 0 12 1 12 2 12 2 0 12 2 例1 设随机变量 (X,Y)的分布律为 求 (1)X Y, (2) X Y 的分布律
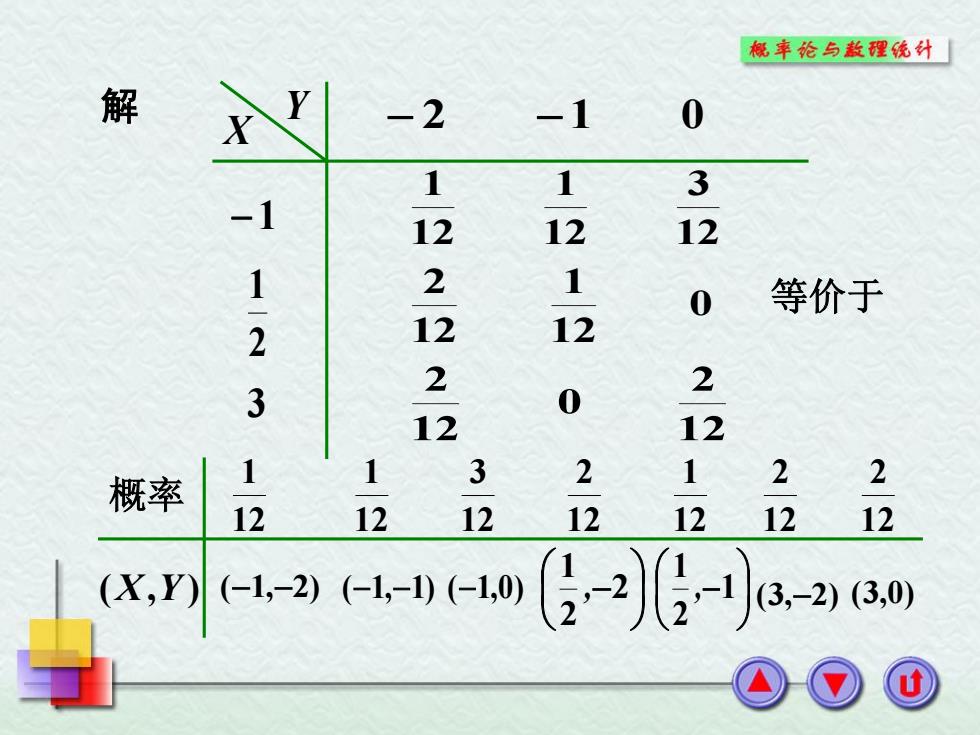
概率论与散理统外「 解 -2 -1 0 1 1 3 -1 12 12 12 1 2 1 0 等价于 2 12 12 3 2 2 0 12 12 概率 1 1 3 2 122 12 12 12 12 1212 12 (X,Y) (-1,-2)(-1,-1)(-1,0) g-2-a2am
概率 ( X , Y ) ( 1 , 2 ) 121 (1,1 ) 121 (1,0) 123 2 21 , 122 1 21 , 121 (3,2) 122 (3,0) 122 X Y 2 1 0 1213 123 121 121 0 121 122 122 0 122 解 等价于

概率论与散理统外 概率 1 1 32 1 2 2 12 1212121212 12 (X,Y-1,-2)(1,-1)←1,0) G-2〔31j3-23w, X+Y-3 - 2-1-3 3 5 3 X-Y 101 53 2
概率 (X,Y ) (1,2) 12 1 (1,1) 12 1 (1,0) 12 3 ,2 2 1 12 2 ,1 2 1 12 1 (3,2) 12 2 (3,0) 12 2 X Y 3 2 1 2 3 2 1 1 3 X Y 1 0 1 2 5 2 3 5 3