
激理方程与特殊函致 第四章行波法(三) 主讲:杨春
第四章 行波法(三) 主讲:杨春

本次课主要内容 一、二维波动方程柯西问题的降维法 二、行波法求解定解问题应用举例
本次课主要内容 一、二维波动方程柯西问题的降维法 二、行波法求解定解问题应用举例

一、二维波动方程柯西问题的降维法 求解:二维空间自由振动波动方程定解问题: u =a 02 (<xy<+o,>0) .)x. 求解方法:把二维看成三维的特殊情形,即把二维情形的方程、初始条件和波函数 看成与z无关的三维问题进行处理,从三维泊松公式出发,利用曲面积分计算,得到 二维问题的解。 三维泊松公式为: u(M,t)=
2 2 2 2 2 2 2 0 0 , , , 0 ( , ) ( , ) t t u u u a x y t t x y u u x y x y t , 求解:二维空间自由振动波动方程定解问题: 求解方法:把二维看成三维的特殊情形,即把二维情形的方程、初始条件和波函数 看成与z无关的三维问题进行处理,从三维泊松公式出发,利用曲面积分计算,得到 二维问题的解。 一、二维波动方程柯西问题的降维法 三维泊松公式为: . . . . 2 1 ( ) ( ) ( , ) 4 M M S S at at M M u M t dS dS a t t t

a (M,t)= (M) 4πa 球面方程为: 5=z±Vat-(5-x)2-(m-y2 将初始条件代入泊松公式,且利用第一型曲面积分公式得到二维柯西问题计算公式: ux.y.t)= (5,) ddn 使用上,一般采用如下极坐标形式: x,y,)= Nar-r r-
球面方程为: 将初始条件代入泊松公式,且利用第一型曲面积分公式得到二维柯西问题计算公式: . . . . 2 1 ( ) ( ) ( , ) 4 M M at at S S M M u M t dS dS a t t t 2 2 2 2 z a t x y ( ) ( ) 2 2 2 2 2 2 2 2 1 ( , ) 1 ( , ) ( , , ) + 2 2 D D ( ) ( ) ( ) ( ) u x y t d d d d a t a a t x y a t x y 使用上,一般采用如下极坐标形式: 2 2 0 0 0 0 2 2 2 2 2 2 1 ( cos , sin ) 1 ( cos , sin ) ( , , ) + 2 2 at at x r y r x r y r u x y t rdrd rdrd a t a a t r a t r
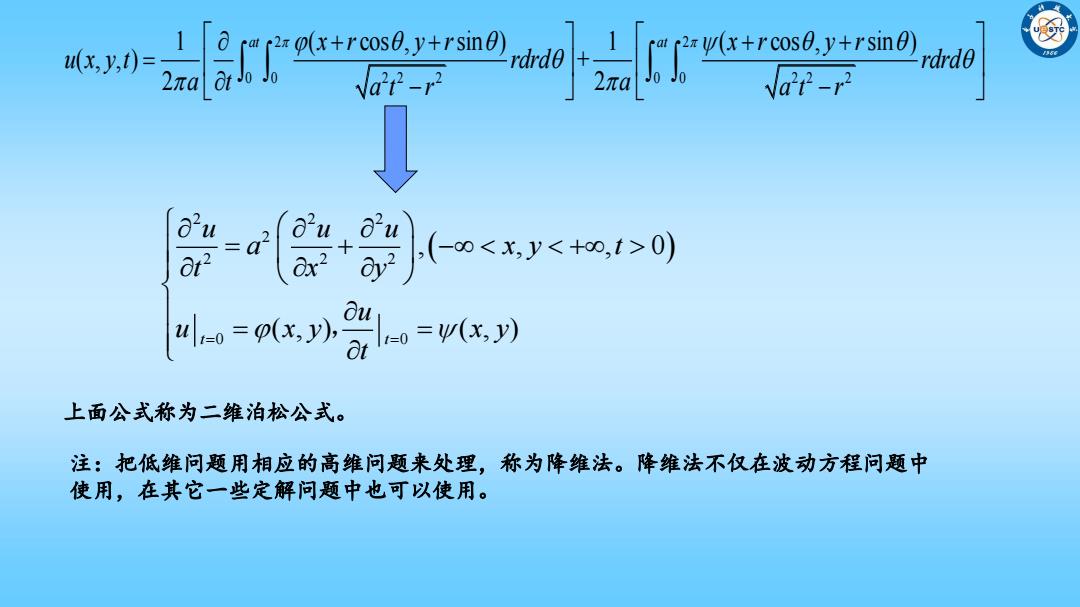
x,y,0= rdrd0 2πa NaP-r a2u d u +0(0<xy<+,1>0) 4L=ox小=n 上面公式称为二维泊松公式。 注:把低维问题用相应的高维问题来处理,称为降维法。降维法不仅在波动方程问题中 使用,在其它一些定解问题中也可以使用
上面公式称为二维泊松公式。 2 2 0 0 0 0 2 2 2 2 2 2 1 ( cos , sin ) 1 ( cos , sin ) ( , , ) + 2 2 at at x r y r x r y r u x y t rdrd rdrd a t a a t r a t r 2 2 2 2 2 2 2 0 0 , , , 0 ( , ) ( , ) t t u u u a x y t t x y u u x y x y t , 注:把低维问题用相应的高维问题来处理,称为降维法。降维法不仅在波动方程问题中 使用,在其它一些定解问题中也可以使用