
定义4设供给函数Q=S(p)可导,则称 AS/So △pPo 为供给函数从p,到p+△p两点间的供给弹性,称 S为债给函数在处的侠给弹佐,记为% 例2设某商品需求量对价格的函数关系为 0=Qp)=80(31 试求需求量Q对价格p的弹性,并说明其经济意义
Q S p = ( ) 0 0 S S p p 0 p 0 p p + 0 0 0 ( ) ( ) p S p S p 0 p s 定义4 设供给函数 可导,则称 两点间的供给弹性,称 为供给函数在 为供给函数从 到 处的供给弹性,记为 . 1 ( ) 800( ) 3 p Q Q p = = 试求需求量 Q 对价格 p 的弹性,并说明其经济意义. 例2 设某商品需求量对价格的函数关系为
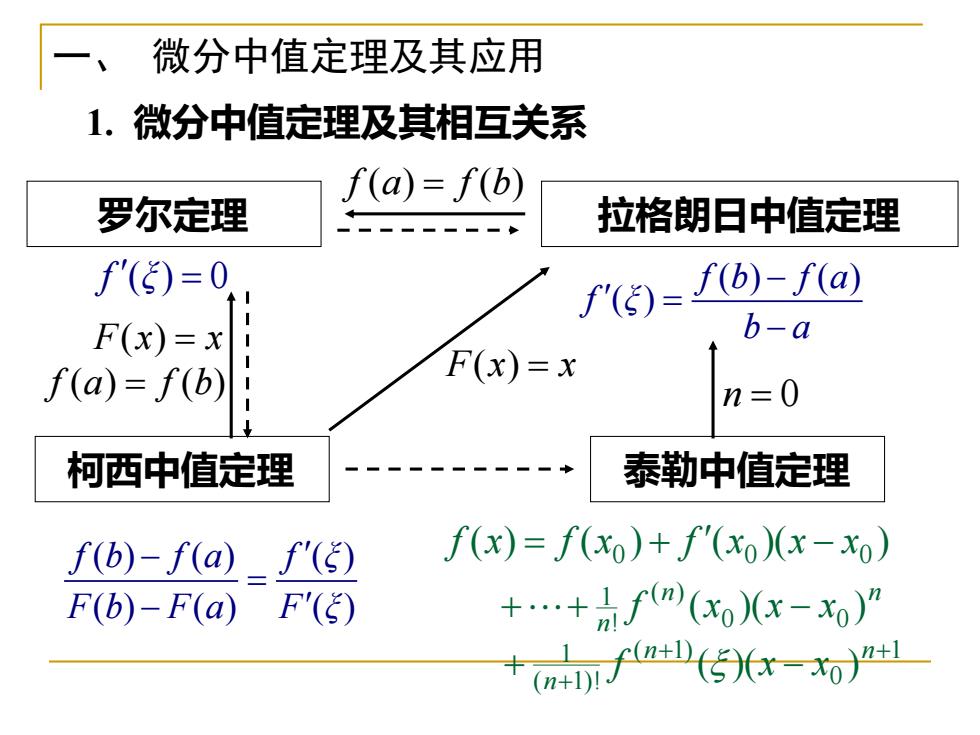
一、微分中值定理及其应用 1.微分中值定理及其相互关系 f(a)=f(b) 罗尔定理 拉格朗日中值定理 f'()=0 M(G)-I(b)-M(a) F(x)=x b-a f(a)=f(b) F(x)=x n=0 柯西中值定理 泰勒中值定理 f(b)-f(a_f'() f(x)=f(xo)+f(xo)(x-x0) F(b)-F(a)F +.+m(x)x-xo)” m子传-o》u
x y O a b y = f (x) 拉格朗日中值定理 f (a) = f (b) 一、 微分中值定理及其应用 1. 微分中值定理及其相互关系 罗尔定理 f ( ) 0 ξ = x y O a b y = f (x) ( ) ( ) ( ) ( ) ( ) ( ) f b f a f ξ F b F a F ξ − = − ( ) ( ) ( ) f b f a f ξ b a − = − 1 0 ( 1) ( 1)! 1 ( )( ) + + + + − n n n f x x F(x) = x 泰勒中值定理 ( ) ( ) ( )( ) 0 0 0 f x = f x + f x x − x n n n f (x )(x x ) 0 0 ( ) ! 1 ++ − n = 0 ( ) ( ) ( ) f a f b F x x = = 柯西中值定理

2.微分中值定理的主要应用 (1)研究函数或导数的性态 (2)证明恒等式或不等式 (3)证明有关中值问题的结论
2. 微分中值定理的主要应用 (1) 研究函数或导数的性态 (2) 证明恒等式或不等式 (3) 证明有关中值问题的结论