
第五节 曲面及其方程2.方程Z给定yOz面上曲线C:f(y,z) = 0 .M(x, y, )Mi(0, Y1, z1)若点 M;(0,y1,z1) EC,则有f(y1,z)) =0 .xy当绕z轴旋转时,该点转到M(x,y,z),则有z=21, Vx?+y2 =|yl,f(±x? +y2 ,2)=0故旋转曲面方程为下页返回MathGS公式数学家上页线与面
第五节 曲面及其方程 2. 方程 x y z M1 (0, y1 , z1 M (x, y, z) ) 故旋转曲面方程为 M (x, y,z) , 当绕 z 轴旋转时, ( , ) 0 . f y1 z1 = (0, , ) , 若点 M1 y1 z1 C 给定 yOz 面上曲线 C: , , 1 2 2 1 则有 z = z x + y = y ( , ) 0 . 2 2 f x + y z = 则有 该点转到 f ( y,z) = 0 . C O

第五节曲面及其方程类似地,可求得yOz面上曲线C:f(y,z)=0,绕y轴旋转所得旋转曲面的方程为f(y,±x?+z?)=0f(x,±/y2+z2)=0f(x,y)=0,绕x轴曲线C:z=0绕y轴f(±Vx? +z?,J)=0f(x,±/y2 +z)=0f(x,z)=0, 绕x轴曲线C:y=0,绕轴f(±V/x? +y2,z)=0MathGS上页下页返回公式数学家线与面
第五节 曲面及其方程 yOz 面上曲线 C:f(y, z)=0,绕y轴旋转所得旋转曲面 类似地,可求得 的方程为 ( , ) 0 . 2 2 f y x + z = 曲线 C: = = 0 , ( , ) 0 , z f x y 绕x轴 ( , ) 0 , 2 2 f x y + z = 绕y轴 ( , ) 0 , 2 2 f x + z y = 曲线 C: = = 0 , ( , ) 0 , y f x z 绕x轴 ( , ) 0 , 2 2 f x y + z = 绕z轴 ( , ) 0 . 2 2 f x + y z =

第五节曲面及其方程例3直线L绕另一条与L相交的直线旋转一周,所得旋转曲面称为圆锥面,两直线的交点称为圆锥面的顶点两直线的夹角α(0<α<元/2)称为圆锥面的半顶角.试建立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面的方程.解包X返回MathGS公式数学家上页下页线与面
第五节 曲面及其方程 第五节 曲面及其方程 解 例3 直线L绕另一条与L相交的直线旋转一周,所得 旋转曲面称为圆锥面,两直线的交点称为圆锥面的顶点 两直线的夹角 (0< < / 2)称为圆锥面的半顶角.试建 立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面 的方程. 直线L 的方程为 z = y cot . 绕 z 轴旋转时,圆锥面的方程为 cot , 2 2 z = x + y ( ) . 2 2 2 2 z = a x + y L x y z O 例3 直线L绕另一条与L相交的直线旋转一周,所得 旋转曲面称为圆锥面, 两直线的交点称为圆锥面的顶点, 两直线的夹角 (0< < / 2)称为圆锥面的半顶角.试建 立顶点在坐标原点、旋转轴为z轴、半顶角为的圆锥面 的方程. L x y z O

第五节曲面及其方程?例4求坐标面xOz上的双曲线=1分别绕x2Oa轴和z轴旋转一周所生成的旋转曲面方程解白例5如图所示的曲面称为圆环面,试建立其方程,并在MathGS中进行验证解白上页返回MathGS公式下页线与面数学家
第五节 曲面及其方程 例4 求坐标面 xOz 上的双曲线 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 第五节 曲面及其方程 例4 求坐标面 xOz 上的双曲线 1 2 2 2 2 − = c z a x 分别绕 x 轴和 z 轴旋转一周所生成的旋转曲面方程. 绕 x 轴旋转 1. 2 2 2 2 2 = + − c y z a x 解 所成曲面方程为 O z x y x y z 第五节 曲面及其方程 例5 如图所示的曲面称为圆环面,试建立其方程, x y z 解 并在MathGS中进行验证. 如图所示的圆环面是 由xOy面上的圆绕y轴旋转所成. 设圆的方程为 ( ) ( ) , 2 2 2 x − a + y −b = R 则圆环面的方程为 ( ) ( ) . 2 2 2 2 2 x + z − a + y −b = R 如图所示的圆环面参数a=b=2,R=0.5. x y z O 例5 如图所示的曲面称为圆环面,试建立其方程, 并在MathGS中进行验证
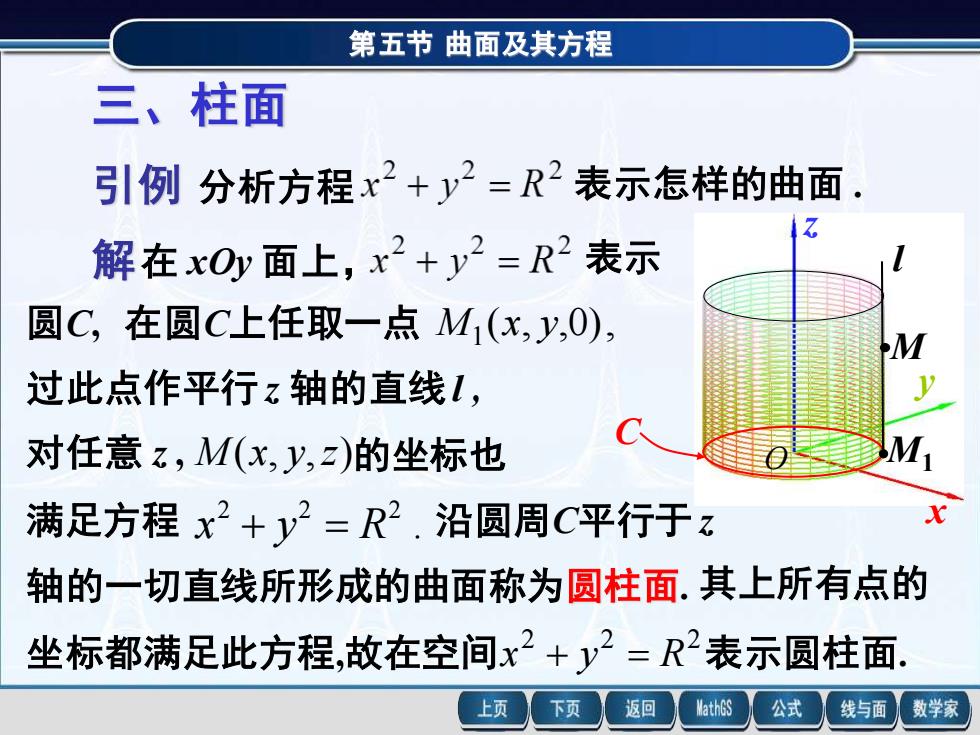
第五节 曲面及其方程三、柱面引例分析方程x2+2=R2表示怎样的曲面Z解在xOy面上,x2+2=R2表示圆C,在圆c上任取一点 M,(x,y,O)M过此点作平行z轴的直线l,V福M对任意 z,M(x,,z)的坐标也x满足方程x2+y=R2.沿圆周C平行于z其上所有点的轴的一切直线所形成的曲面称为圆柱面坐标都满足此方程,故在空间x2+y2= R2表示圆柱面.返回MathGS公式数学家上页下页线与面
第五节 曲面及其方程 引例 分析方程 表示怎样的曲面 . 的坐标也 在 xOy 面上, . 2 2 2 x + y = R 沿圆周C平行于 z 坐标都满足此方程,故在空间 2 2 2 x + y = R 轴的一切直线所形成的曲面称为圆柱面. 对任意 z , 过此点作平行 z 轴的直线l , 表示圆柱面. 圆C, ( , ,0), 1 M x y M (x, y,z) 其上所有点的 三、柱面 x y z M M1 满足方程 解 表示 在圆C上任取一点 l C O