
概车纶与款理统外 第四节 区间估计 一、区间估计的基本概念 二、典型例题
第四节 区间估计 一、区间估计的基本概念 二、典型例题

概率伦与款醒统外 一、 区间估计的基本概念 1.置信区间的定义 设总体X的分布函数F(x;)含有一个未知参 数0,对于给定值a(0<a<1),若由样本X1,X2,., X,确定的两个统计量 0=(X1,X2,.,Xm)和0=0(X1,X2,.,Xm)满足 P{0(X1,X2,Xn)<0<0X1,X2,Xn)}=1-a, 则称随机区间,0)是0的置信度为-a的置信区 间,Q和分别称为置信度为-α的双侧置信区间 的置信下限和置信上限1-a为置信度
一、区间估计的基本概念 1. 置信区间的定义 { ( , , , ) ( , , , )} 1 , ( , , , ) ( , , , ) , (0 1), , , , ( ; ) 1 2 1 2 1 2 1 2 1 2 = − = = n n n n n P X X X X X X X X X X X X X X X X F x 和 满 足 确定的两个统计量 数 对于给定值 若由样本 设总体 的分布函数 含有一个未知参 , 1 . , 1 ( , ) 1 的置信下限和置信上限 为置信度 间 和 分别称为置信度为 的双侧置信区间 则称随机区间 是 的置信度为 的置信区 − − −

概车纶与款理统外 关于定义的说明 被估计的参数虽然未知,但它是一个常数, 没有随机性,而区间(Q,0)是随机的. 因此定义中下表达式 P{0(X1,X2,.,Xn)<0<0(X1,X2,Xn)}=1-a 的本质是: 随机区间(,0)以1-a的概率包含着参数的真值, 而不能说参数以1-a的概率落入随机区间(日,8)
关于定义的说明 , ( , ) . , , 没有随机性 而区间 是随机的 被估计的参数 虽然未知 但它是一个常数 : { ( , , , ) ( , , , )} 1 1 2 1 2 的本质是 因此定义中下表达式 P X X Xn X X Xn = − 1 ( , ). ( , ) 1 , 而不能说参数 以 的概率落入随机区间 随机区间 以 的概率包含着参数 的真值 − −

概華论与款醒硫外「 另外定义中的表达式 P{0(X1,X2,Xn)<B<8(X1,X2,Xn)}=1-a 还可以描述为: 若反复抽样多次(各次得到的样本容量相等,都是) 每个样本值确定一个区间(,日), 每个这样的区间或包含0的真值或不包含0的真值, 按伯努利大数定理,在这样多的区间中, 包含真值的约占100(1-)%,不包含的约占100a%
: { ( , , , ) ( , , , )} 1 1 2 1 2 还可以描述为 另外定义中的表达式 P X X Xn X X Xn = − 若反复抽样多次(各次得到的样本容量相等,都是n) 每个样本值确定一个区间( , ), 按伯努利大数定理, 在这样多的区间中, 包含真值的约占100(1−)%,不包含的约占100%. 每个这样的区间或包含 的真值或不包含 的真值
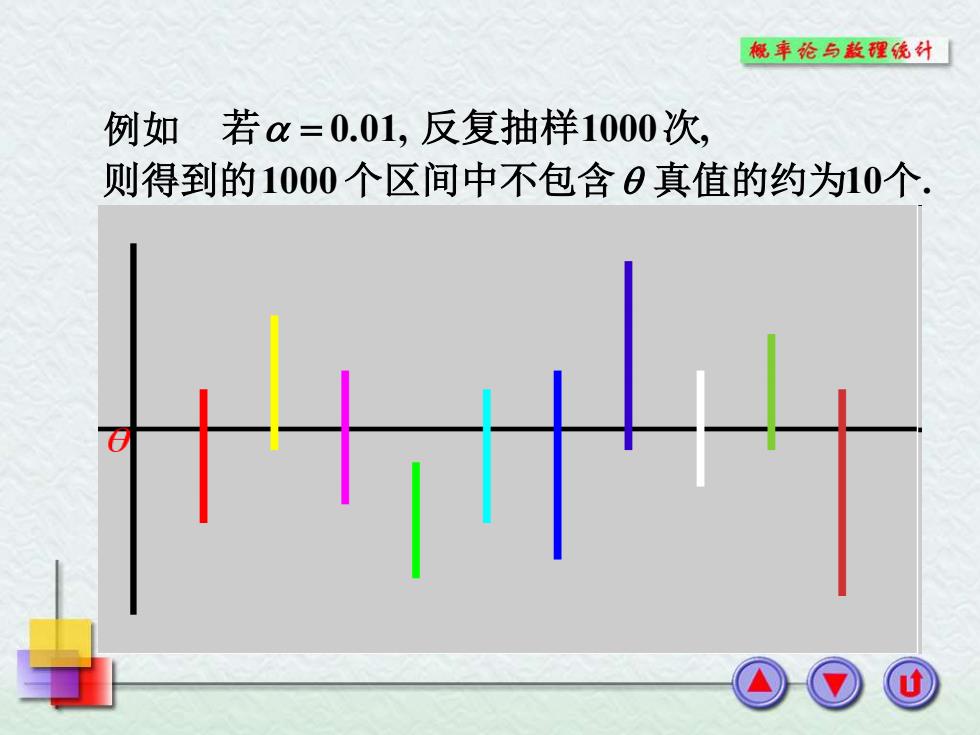
概车纶与款理统外 例如若=0.01,反复抽样1000次 则得到的1000个区间中不包含0真值的约为10个
例如 若 = 0.01, 反复抽样1000次, 则得到的1000个区间中不包含 真值的约为10个