
第三节导数的应用渐近线函数图形的描绘小结思考题高等数学(上册)
渐近线 第三节 导数的应用 小结 思考题 函数图形的描绘

一、渐近线(asymptotes)定义当曲线y=f(x)上的一动点P沿着曲线移向无穷点时,如果点P到某定直线L的距离趋向于零,那么直线L就称为曲线y=f(x)的一条渐近线(垂直于x轴的渐近线)1.铅直渐近线如果lim f(x)=0 或 lim_f(x)= 80x→xxx那么x=x,就是y= f(x)的一条铅直渐近线11如y=(=8lim(x + 2)(x - 3)x=-2 (x + 2)(x - 3)1=8lim铅直渐近线:x=-2,x=3x-3 (x + 2)(x -3)高等数学(上册)
定义 当曲线y f (x)上的一动点P沿着曲线 1. 铅直渐近线 如果 移向无穷点时,如果点 P 到某定直线 L的距离 趋向于零,那么直线 L 就称为曲线 y f (x)的 那么 x x0 x x0就是y f (x)的一条 一、渐近线(asymptotes) 铅直渐近线. lim f (x) 或 lim f (x) x x0 一条渐近线. 如 , ( 2)( 3) 1 x x y 铅直渐近线:x 2, ( 2)( 3) 1 lim x2 x x ( 2)( 3) 1 lim x3 x x x 3. (垂直于x轴的渐近线)
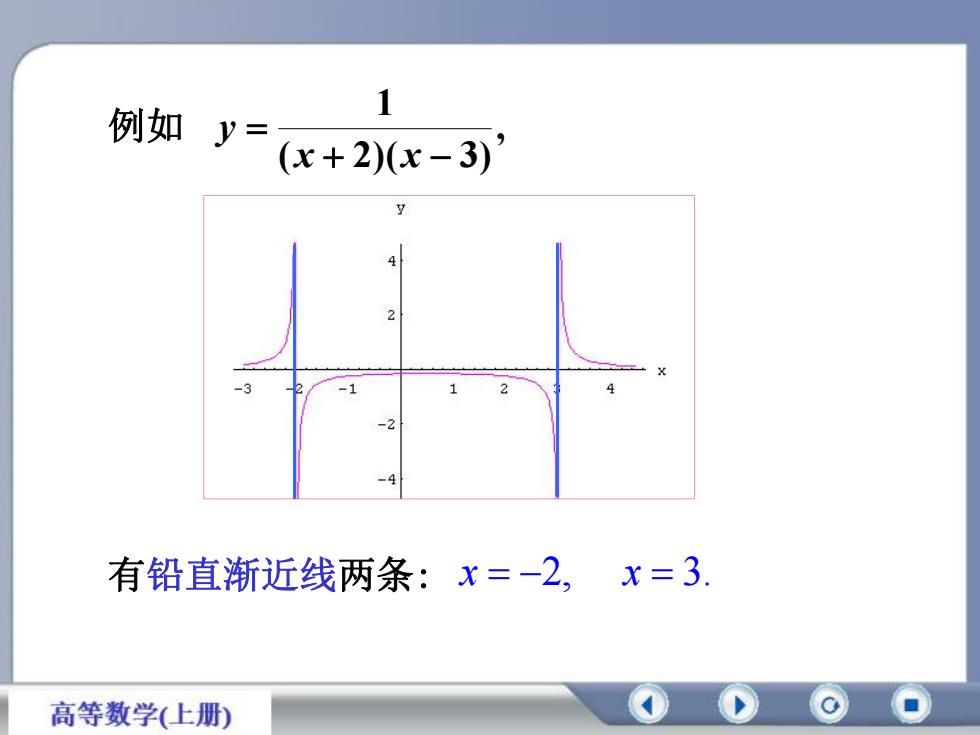
1例如y:(x + 2)(x - 3)V212-1.-2x = 3.有铅直渐近线两条:x=-2,高等数学(上册)
例如 , ( 2)( 3) 1 x x y 有铅直渐近线两条: x 2, x 3
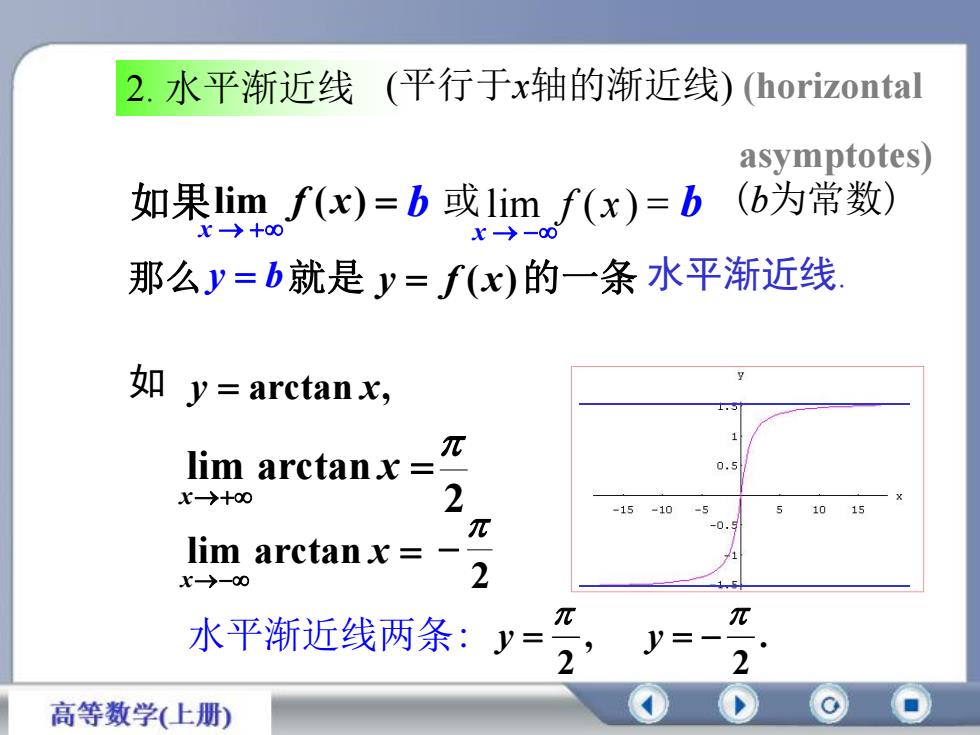
(平行于x轴的渐近线)(horizontal2.水平渐近线asymptotes如果limf(x)=b 或lim f(x)=b (b为常数)x→+8x→那么=b就是=f(x)的一条水平渐近线如 y= arctanx,元lim arctanx =0.52x-→+-5510151015元-0.lim arctanx =2x→-80元元水平渐近线两条:22一高等数学(上册)
2. 水平渐近线 如果 如 y arctan x, 水平渐近线两条: , 2 y x x lim arctan x x lim arctan 那么 . 2 y lim f (x) y b就是 y f (x)的一条 水平渐近线. x x b 或 b (b为常数) 2 2 (平行于x轴的渐近线) (horizontal asymptotes) lim f ( x )

3.斜渐近线(inclined asymptotes)如果lim [f(x)- (ax +b)] = 0X或 lim[f(x)-(ax+b)]=0(a,b为常数)X→-那么=ax+b就是=f(x)的一条斜渐近线下面求计算a,b的公式: lim ={f(x)-(ax+b)=0由上式和x为无穷大,有x→00Xf(x)f(x)bJima=0即 limx→±0x10xx斜渐近线求法:f(x)lima=l求出a后,将a代入可确定b,x→±xb = lim [f(x) -ax]高等那上ax+b就是曲线y=f(x)的一条斜渐近线
(inclined asymptotes) lim [ ( ) ( )] 0 lim [ ( ) ( )] 0 ( , ) ( ) . x x f x ax b f x a y x b a b ax b y f x 如果 或 为常数 那么 就是 的一条斜渐近线 斜渐近线求法: 那么 y ax b 就是曲线 y f (x)的一条斜渐近线. 3. 斜渐近线 求出a后, b lim [ f (x) ax] x x f x a x ( ) lim 将a代入可确定b, 下面求计算 a,b的公式 : 由上式和 [ ( ) ( )] 0 1 lim f x ax b x x x为无穷大, ] ( ) lim [ x b a x f x x a x f x x ( ) lim 0 有 即