
第五节函数的极值与最大值最小值最大值最小值问题作业小结思考题第三章 微分中值定理与导数的应用高等数学(上册)
1 小结 思考题 作业 最大值最小值问题 第五节 函数的极值与 最大值最小值 第三章 微分中值定理与导数的应用
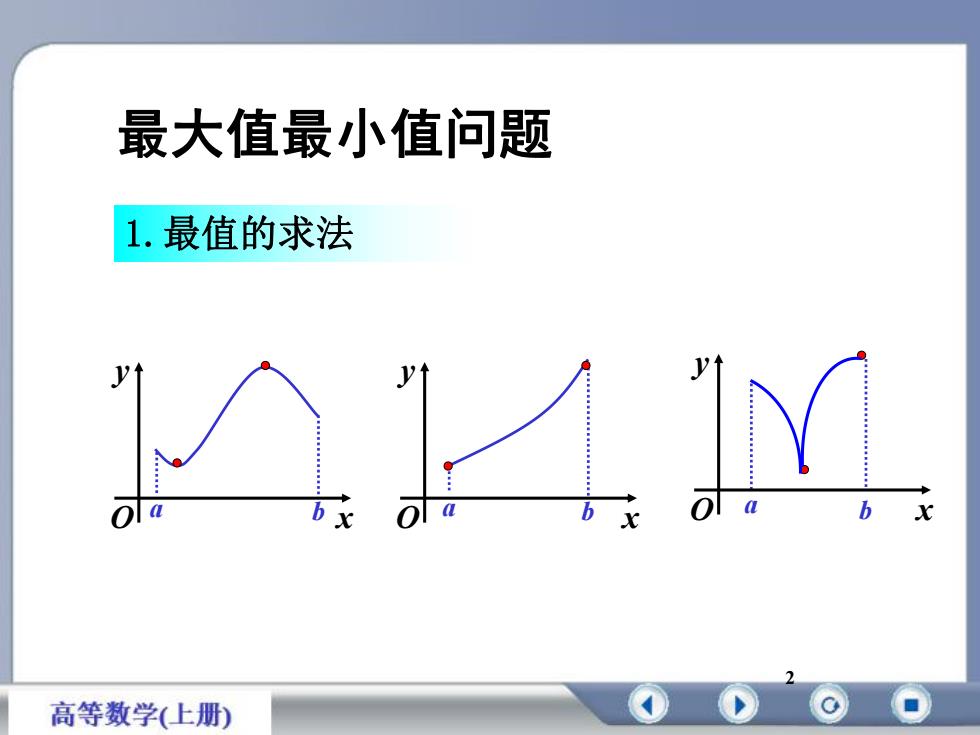
最大值最小值问题1.最值的求法olabaxabolh0xx高等数学(上册)
2 a b a b a b 最大值最小值问题 1.最值的求法 x y O x y O x y O
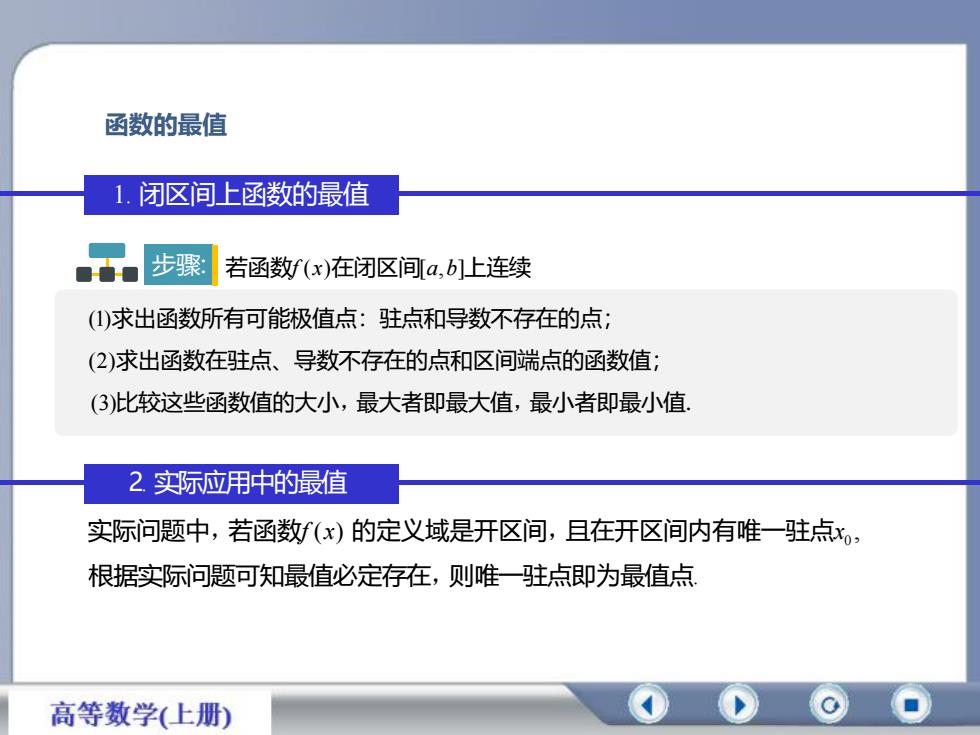
函数的最值1.闭区间上函数的最值步骤若函数f(x)在闭区间[a,b]上连续(1)求出函数所有可能极值点:驻点和导数不存在的点;(2)求出函数在驻点、导数不存在的点和区间端点的函数值:(3)比较这些函数值的大小,最大者即最大值,最小者即最小值2.实际应用中的最值实际问题中,若函数f(x)的定义域是开区间,且在开区间内有唯一驻点xo:根据实际问题可知最值必定存在,则唯一驻点即为最值点高等数学(上册)
函数的最值 1. 闭区间上函数的最值 2. 实际应用中的最值 0 实际问题中,若函数f (x) 的定义域是开区间,且在开区间内有唯一驻点x , 根据实际问题可知最值必定存在,则唯一驻点即为最值点. (1)求出函数所有可能极值点:驻点和导数不存在的点; (2)求出函数在驻点、导数不存在的点和区间端点的函数值; (3)比较这些函数值的大小,最大者即最大值,最小者即最小值. 步骤: 若函数f (x)在闭区间[a,b]上连续

2.应用举例例1求函数V=2x3+3x2-12x+14的在[-3.41上的最大值与最小值解 : f'(x) = 6(x + 2)(x -1)解方程 f'(x)=0,得 xi =-2,x, =1.计算f(-3)=23;f(-2) =34;f(1) =7;f(4) =142;y=2x+3x2-12x+14比较得最大值f(4)=142,最小值 f(1)= 7.高等数学(上册)
例1 解 f ( x) 6( x 2)(x 1) 3 2 求函数 y 2x 3x 12x 14的在[3, 4]上的最大值与最小值. 解方程 f ( x) 0,得 2, 1. x1 x2 计算 f (3) 23; f (2) 34; f (1) 7; f (4) 142; 比较得 最大值 f (4) 142, 最小值 f (1) 7. 2 3 12 14 3 2 y x x x 2. 应用举例

函数的最值将边长为α的一正方形铁皮,四角各截去一个大小相同的小正方形,然后将R四边折起做一个无盖的方盒.问截掉的小正方形边长多大时,所得方盒容积最大?福解设截掉的小正方形边长为x,则方盒底面是边长为α-2x的正方形故方盒容积为y=x(a-2x),xe[0.号)2aa(舍去)令y=(2x-a)(6x-a)=0得驻点x-2N6-4α<0知x=~为极大值点,由此时y6又驻点唯一,故极大值点就是最大值点,即截掉的小正方形边长为一时,所得方盒容积最大,65高等数学(上册)
函数的最值 5 将边长为a 的一正方形铁皮,四角各截去一个大小相同的小正方形,然后将 四边折起做一个无盖的方盒.问截掉的小正方形边长多大时,所得方盒容积最大? 设截掉的小正方形边长为x ,则方盒底面是边长为a 2 x 的正方形, 2 2 0, . 2 a y x a x x 故方盒容积为 , 1 2 6 0 ( ). 6 a a 令y x a x a 得驻点x ,x2 舍去 2 又驻点唯一,故极大值点就是最大值点,即 1 4 0 6 6 a a y a x 由此时 知 为极大值点, 6 a 截掉的小正方形边长为 时,所得方盒容积最大. 例 解