
第三节导数的应用函数的极值小结思考题高等数学(上册)
函数的极值 第三节 导数的应用 小结 思考题
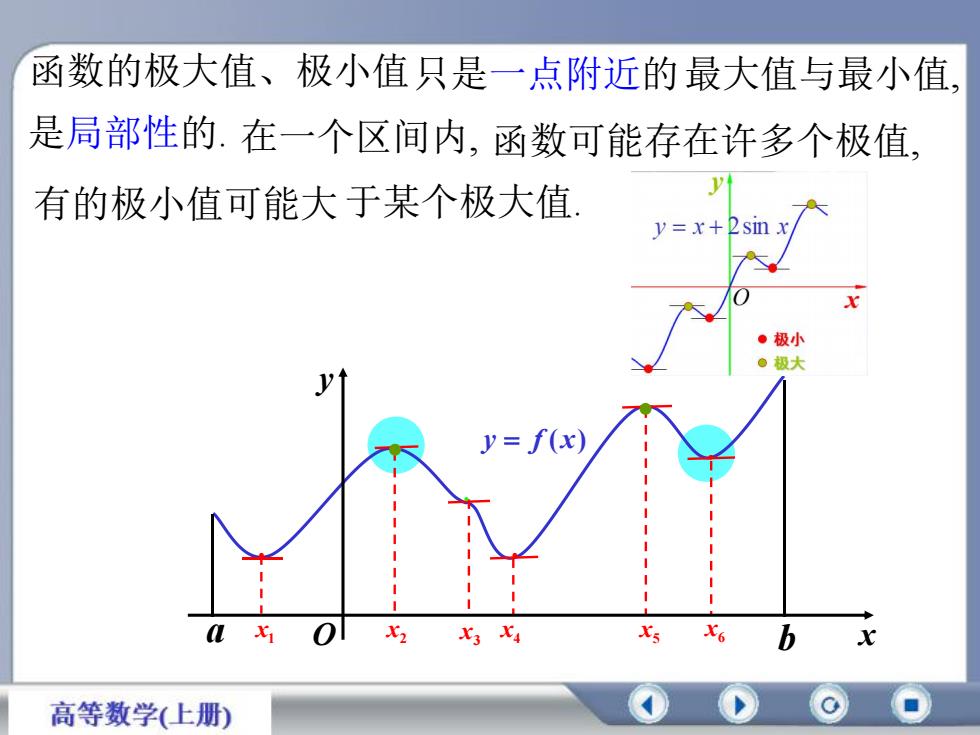
函数的极大值、极小值只是一点附近的最大值与最小值是局部性的.在一个区间内,函数可能存在许多个极值有的极小值可能大于某个极大值y=x+sinxx·极小极大6y=f(x)olX6X2baXiXsX3Xx高等数学(上册)
x1 x2 x3 x4 x5 x6 函数的极大值、极小值 是局部性的. 在一个区间内, 函数可能存在许多个极值, 最大值与最小值, 有的极小值可能大 于某个极大值. 只是一点附近的 x y a O b y f ( x)

使导数f(x)为零的点叫做函数f(x)的驻点极值的必要条件2极值点驻点定理1(必要条件)1.如果函数f(x)在点x,处取得极值,且在x,处可导,则必有f(x)=0注((1)可导函数的极值点必是驻点,但函数的J=x3驻点却不一定是极值点y如, y=x3, |x=0 = 0,x但x=0不是极值点高等数学(上册)
定理1(必要条件) 注 如, , 3 y x 0, y x0 但x 0不是极值点. (1) 如果函数f ( x)在点x0处取得 , 且在x0处可导 叫做函数 的 使导数 为零的点 ( ) ( ) f x f x 驻点. 可导函数的极值点 驻点却不一定是极值点. 但函数的 2. 极值的必要条件 必是驻点, 0 极值, 则必有f (x ) 0. 3 y x x y O 极值点驻点

(2)极值点也可能是导数不存在的点Dy=/x?如,=2,x=0是极小值点但=x2在x=0不可导0x高等数学(上册)
x yO 3 2 y x 极值点也可能是导数不存在的点. 如, , 3 2 y x 3 2 但 y x (2) 不可导. x 0 是极小值点. 在x 0
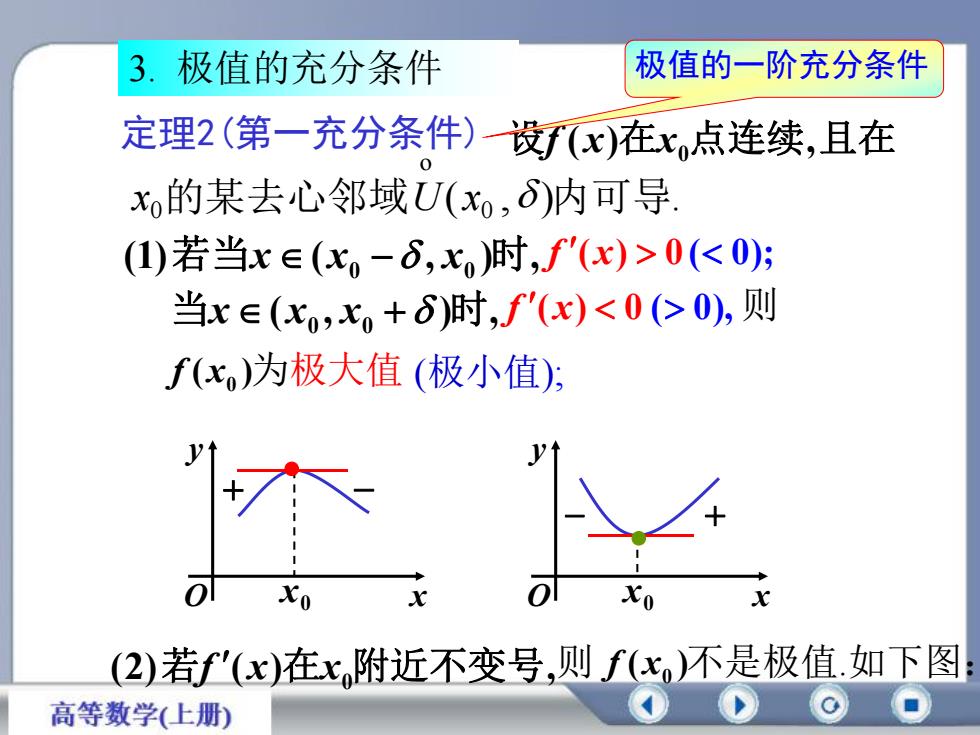
极值的一阶充分条件极值的充分条件3定理2(第一充分条件)一设f(x)在x,点连续,且在xo的某去心邻域U(xo,)内可导(1)若当x E (x。-S,x)时,f'(x)>0(<0);当x E (xo,X。 +8)时,f'(x)<0 (> 0),则f(x)为极大值 (极小值);yyototxoxoxx(2)若f(x)在x,附近不变号,则f(x)不是极值.如下图高等数学(上册)
定理2(第一充分条件) 设f (x)在x0点连续,且在 (1) ( , ) , 若当x x0 x0 时 f (x) 0( 0); ( , ) , 当x x0 x0 时 f (x) 0 ( 0), 则 ( ) x0 f 为极大值 (2) ( ) , 若f x 在x0附近不变号 ( ) x0 则 f 不是极值.如下图: (极小值); 3. 极值的充分条件 极值的一阶充分条件 x y O x0 x y O x0 ( , ) . 0 o x0的某去心邻域U x 内可导